Fast Cosine Similarity Search in Binary Space with Angular Multi-index Hashing
Paper and Code
Apr 18, 2018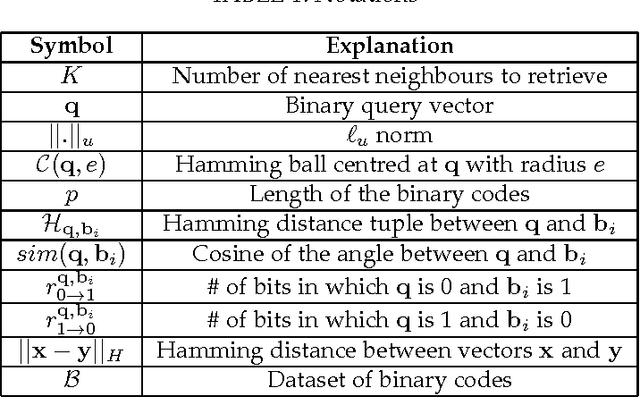
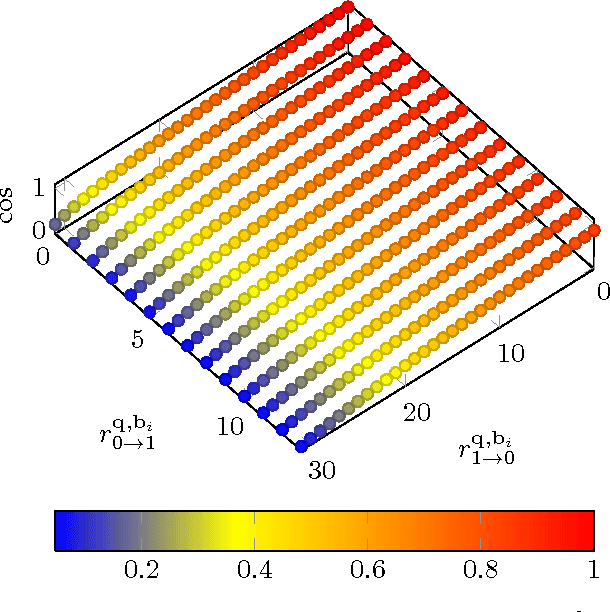
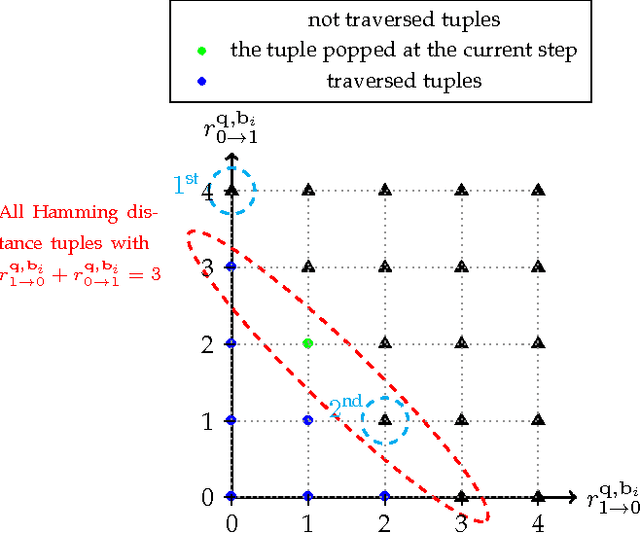
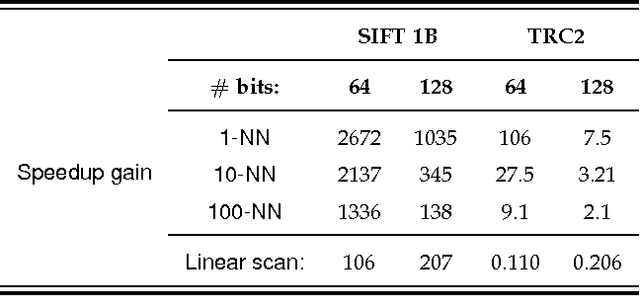
Given a large dataset of binary codes and a binary query point, we address how to efficiently find $K$ codes in the dataset that yield the largest cosine similarities to the query. The straightforward answer to this problem is to compare the query with all items in the dataset, but this is practical only for small datasets. One potential solution to enhance the search time and achieve sublinear cost is to use a hash table populated with binary codes of the dataset and then look up the nearby buckets to the query to retrieve the nearest neighbors. However, if codes are compared in terms of cosine similarity rather than the Hamming distance, then the main issue is that the order of buckets to probe is not evident. To examine this issue, we first elaborate on the connection between the Hamming distance and the cosine similarity. Doing this allows us to systematically find the probing sequence in the hash table. However, solving the nearest neighbor search with a single table is only practical for short binary codes. To address this issue, we propose the angular multi-index hashing search algorithm which relies on building multiple hash tables on binary code substrings. The proposed search algorithm solves the exact angular $K$ nearest neighbor problem in a time that is often orders of magnitude faster than the linear scan baseline and even approximation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge