Fast Approximate Bayesian Computation for Estimating Parameters in Differential Equations
Paper and Code
Jul 17, 2015
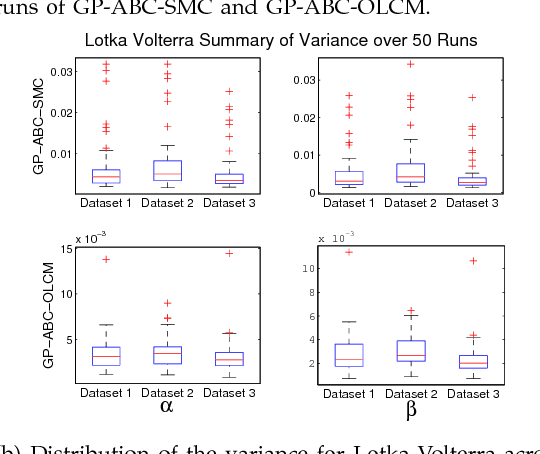
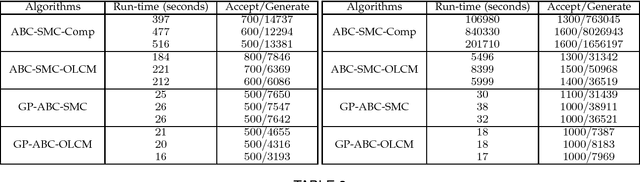
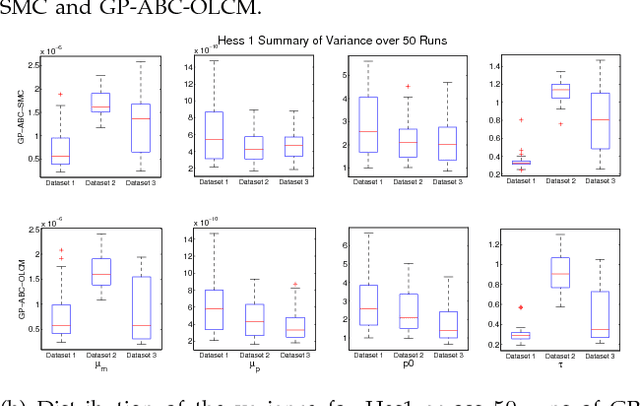
Approximate Bayesian computation (ABC) using a sequential Monte Carlo method provides a comprehensive platform for parameter estimation, model selection and sensitivity analysis in differential equations. However, this method, like other Monte Carlo methods, incurs a significant computational cost as it requires explicit numerical integration of differential equations to carry out inference. In this paper we propose a novel method for circumventing the requirement of explicit integration by using derivatives of Gaussian processes to smooth the observations from which parameters are estimated. We evaluate our methods using synthetic data generated from model biological systems described by ordinary and delay differential equations. Upon comparing the performance of our method to existing ABC techniques, we demonstrate that it produces comparably reliable parameter estimates at a significantly reduced execution time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge