Fast and Robust Sparsity Learning over Networks: A Decentralized Surrogate Median Regression Approach

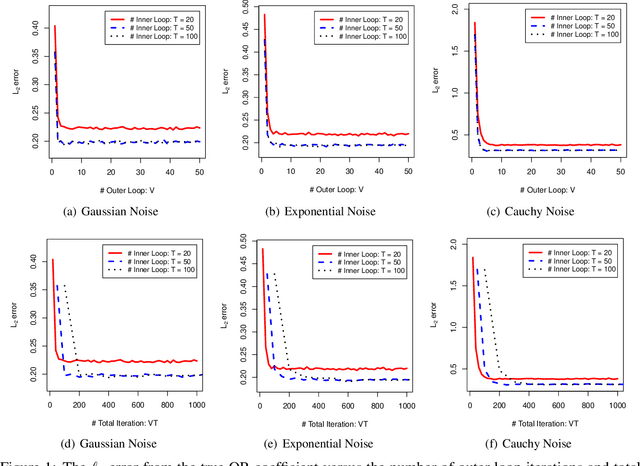
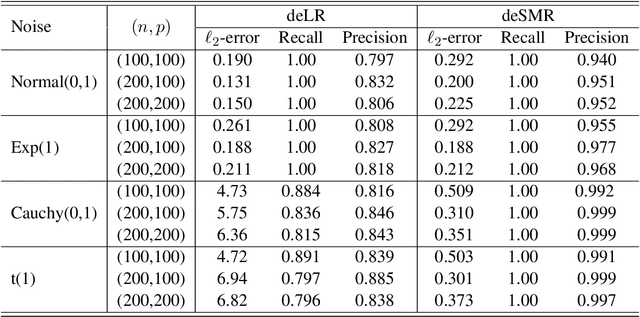
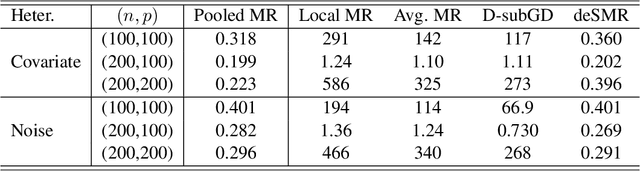
Decentralized sparsity learning has attracted a significant amount of attention recently due to its rapidly growing applications. To obtain the robust and sparse estimators, a natural idea is to adopt the non-smooth median loss combined with a $\ell_1$ sparsity regularizer. However, most of the existing methods suffer from slow convergence performance caused by the {\em double} non-smooth objective. To accelerate the computation, in this paper, we proposed a decentralized surrogate median regression (deSMR) method for efficiently solving the decentralized sparsity learning problem. We show that our proposed algorithm enjoys a linear convergence rate with a simple implementation. We also investigate the statistical guarantee, and it shows that our proposed estimator achieves a near-oracle convergence rate without any restriction on the number of network nodes. Moreover, we establish the theoretical results for sparse support recovery. Thorough numerical experiments and real data study are provided to demonstrate the effectiveness of our method.