Fast and Accurate Low-Rank Factorization of Compressively-Sensed Data

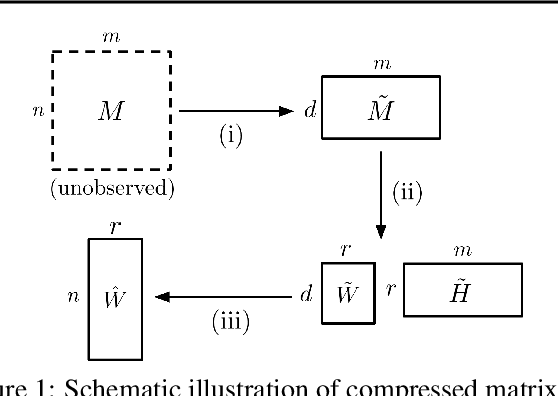
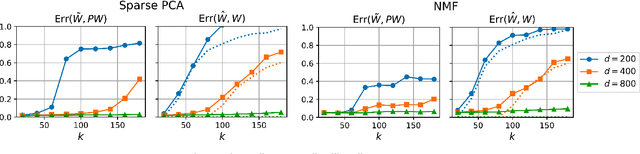
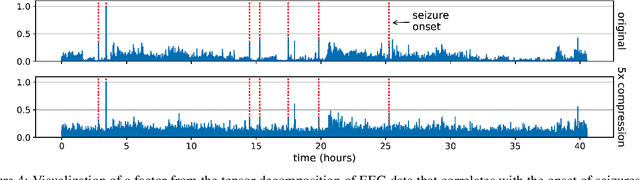
We consider the question of accurately and efficiently computing low-rank matrix or tensor factorizations given data compressed via random projections. This problem arises naturally in the many settings in which data is acquired via compressive sensing. We examine the approach of first performing factorization in the compressed domain, and then reconstructing the original high-dimensional factors from the recovered (compressed) factors. In both the tensor and matrix settings, we establish conditions under which this natural approach will provably recover the original factors. We support these theoretical results with experiments on synthetic data and demonstrate the practical applicability of our methods on real-world gene expression and EEG time series data.