Fairness in Forecasting and Learning Linear Dynamical Systems

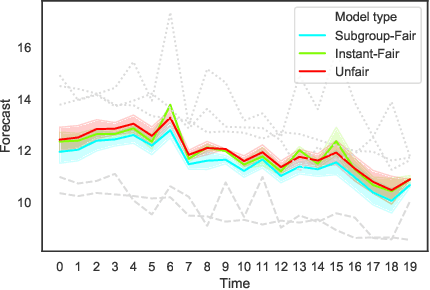
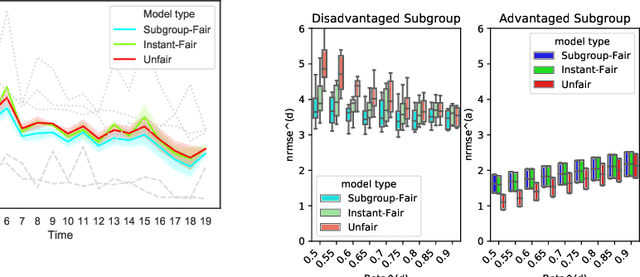
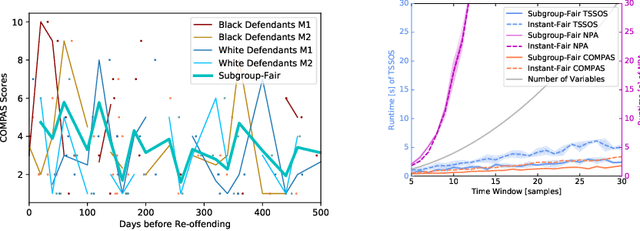
As machine learning becomes more pervasive, the urgency of assuring its fairness increases. Consider training data that capture the behaviour of multiple subgroups of some underlying population over time. When the amounts of training data for the subgroups are not controlled carefully, under-representation bias may arise. We introduce two natural concepts of subgroup fairness and instantaneous fairness to address such under-representation bias in forecasting problems. In particular, we consider the learning of a linear dynamical system from multiple trajectories of varying lengths, and the associated forecasting problems. We provide globally convergent methods for the subgroup-fair and instant-fair estimation using hierarchies of convexifications of non-commutative polynomial optimisation problems. We demonstrate both the beneficial impact of fairness considerations on the statistical performance and the encouraging effects of exploiting sparsity on the estimators' run-time in our computational experiments.