FAIRM: Learning invariant representations for algorithmic fairness and domain generalization with minimax optimality
Paper and Code
Apr 02, 2024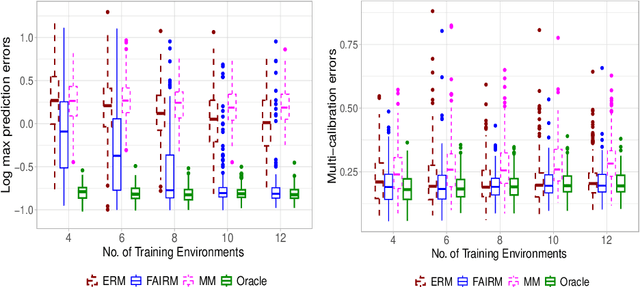
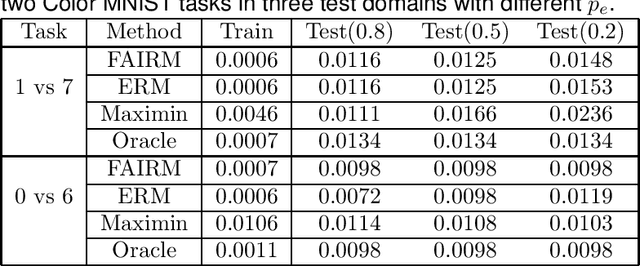
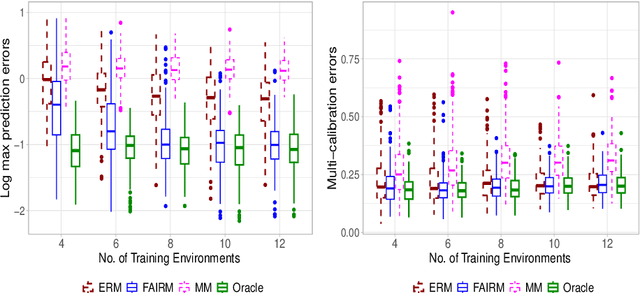
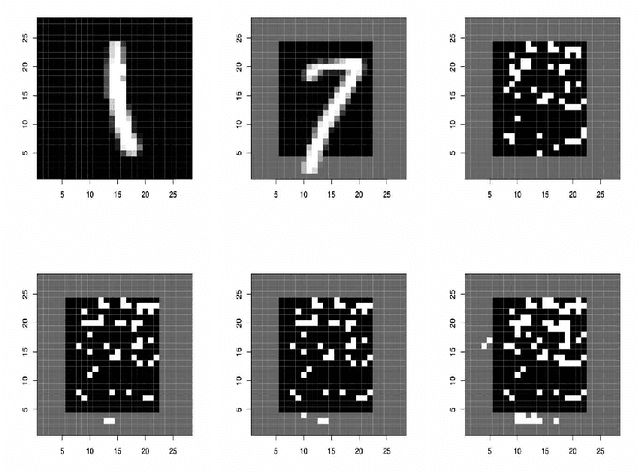
Machine learning methods often assume that the test data have the same distribution as the training data. However, this assumption may not hold due to multiple levels of heterogeneity in applications, raising issues in algorithmic fairness and domain generalization. In this work, we address the problem of fair and generalizable machine learning by invariant principles. We propose a training environment-based oracle, FAIRM, which has desirable fairness and domain generalization properties under a diversity-type condition. We then provide an empirical FAIRM with finite-sample theoretical guarantees under weak distributional assumptions. We then develop efficient algorithms to realize FAIRM in linear models and demonstrate the nonasymptotic performance with minimax optimality. We evaluate our method in numerical experiments with synthetic data and MNIST data and show that it outperforms its counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge