Fair Classification with Adversarial Perturbations
Paper and Code
Jun 10, 2021
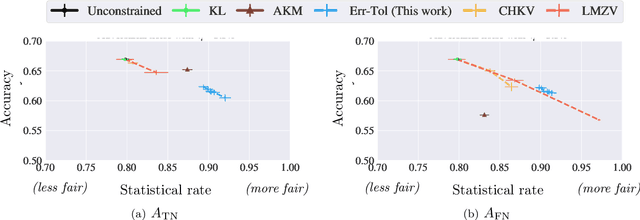
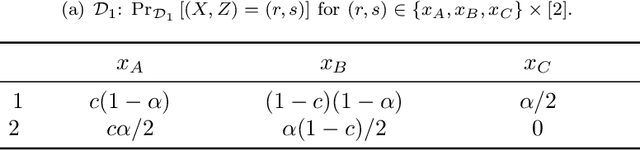
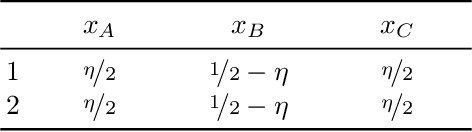
We study fair classification in the presence of an omniscient adversary that, given an $\eta$, is allowed to choose an arbitrary $\eta$-fraction of the training samples and arbitrarily perturb their protected attributes. The motivation comes from settings in which protected attributes can be incorrect due to strategic misreporting, malicious actors, or errors in imputation; and prior approaches that make stochastic or independence assumptions on errors may not satisfy their guarantees in this adversarial setting. Our main contribution is an optimization framework to learn fair classifiers in this adversarial setting that comes with provable guarantees on accuracy and fairness. Our framework works with multiple and non-binary protected attributes, is designed for the large class of linear-fractional fairness metrics, and can also handle perturbations besides protected attributes. We prove near-tightness of our framework's guarantees for natural hypothesis classes: no algorithm can have significantly better accuracy and any algorithm with better fairness must have lower accuracy. Empirically, we evaluate the classifiers produced by our framework for statistical rate on real-world and synthetic datasets for a family of adversaries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge