Facilitating Bayesian Continual Learning by Natural Gradients and Stein Gradients
Paper and Code
Apr 24, 2019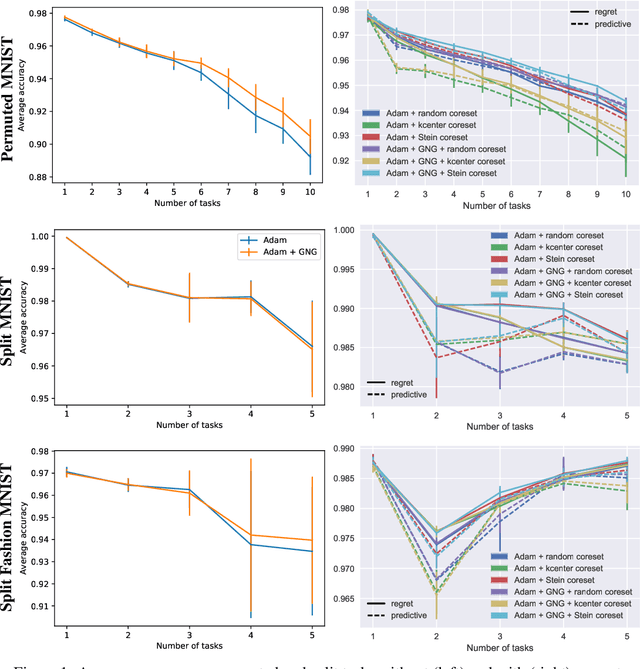
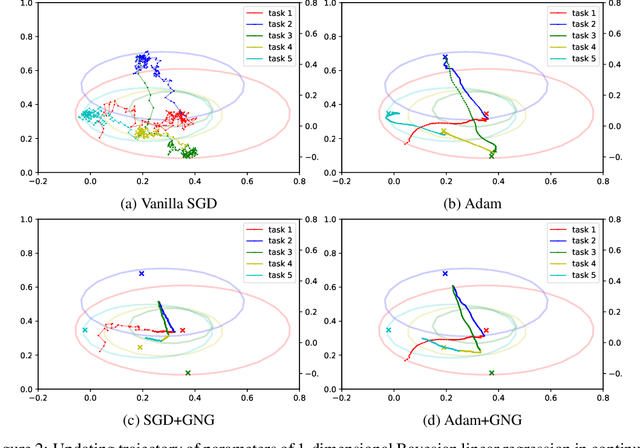
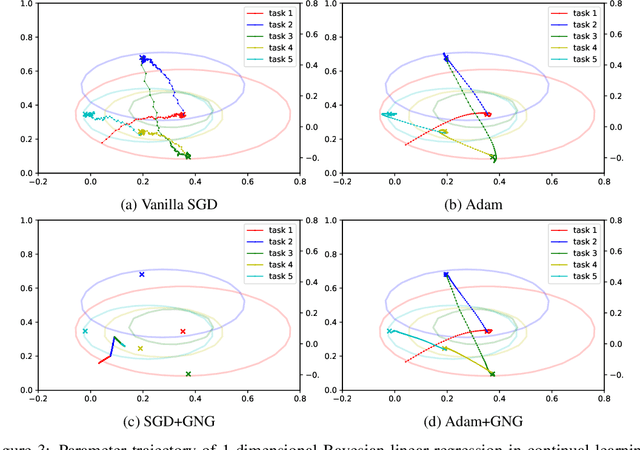
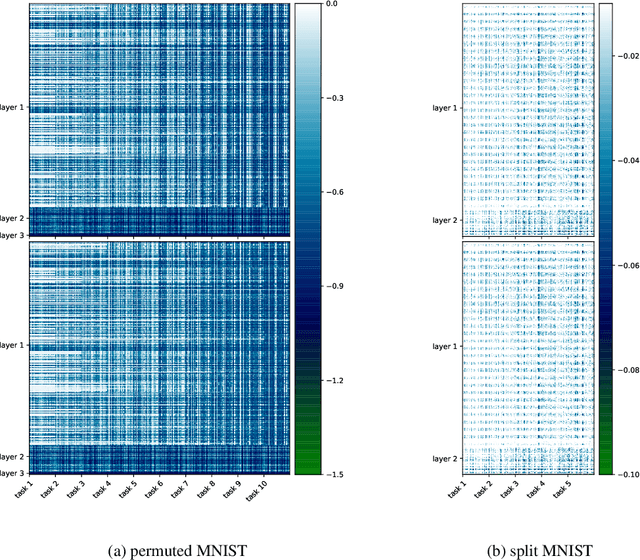
Continual learning aims to enable machine learning models to learn a general solution space for past and future tasks in a sequential manner. Conventional models tend to forget the knowledge of previous tasks while learning a new task, a phenomenon known as catastrophic forgetting. When using Bayesian models in continual learning, knowledge from previous tasks can be retained in two ways: 1). posterior distributions over the parameters, containing the knowledge gained from inference in previous tasks, which then serve as the priors for the following task; 2). coresets, containing knowledge of data distributions of previous tasks. Here, we show that Bayesian continual learning can be facilitated in terms of these two means through the use of natural gradients and Stein gradients respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge