F-measure Maximization in Multi-Label Classification with Conditionally Independent Label Subsets
Paper and Code
Jul 01, 2016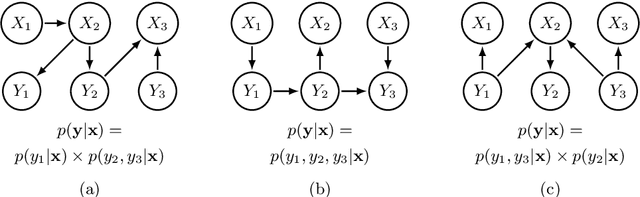
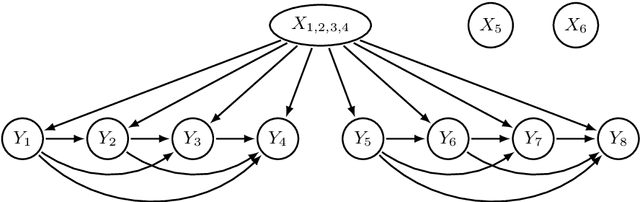
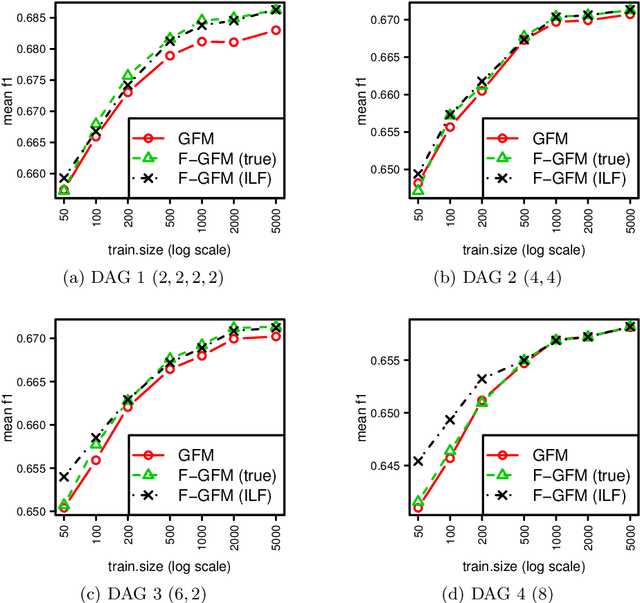
We discuss a method to improve the exact F-measure maximization algorithm called GFM, proposed in (Dembczynski et al. 2011) for multi-label classification, assuming the label set can be can partitioned into conditionally independent subsets given the input features. If the labels were all independent, the estimation of only $m$ parameters ($m$ denoting the number of labels) would suffice to derive Bayes-optimal predictions in $O(m^2)$ operations. In the general case, $m^2+1$ parameters are required by GFM, to solve the problem in $O(m^3)$ operations. In this work, we show that the number of parameters can be reduced further to $m^2/n$, in the best case, assuming the label set can be partitioned into $n$ conditionally independent subsets. As this label partition needs to be estimated from the data beforehand, we use first the procedure proposed in (Gasse et al. 2015) that finds such partition and then infer the required parameters locally in each label subset. The latter are aggregated and serve as input to GFM to form the Bayes-optimal prediction. We show on a synthetic experiment that the reduction in the number of parameters brings about significant benefits in terms of performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge