Exposure-Referred Signal-to-Noise Ratio for Digital Image Sensors
Paper and Code
Dec 10, 2021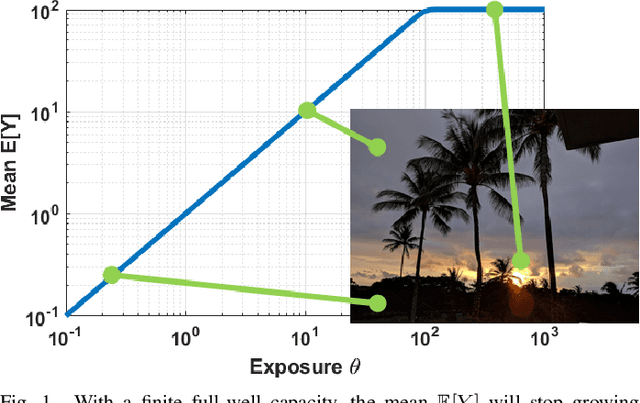
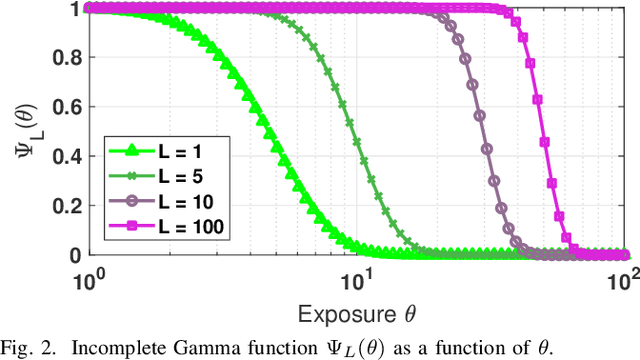

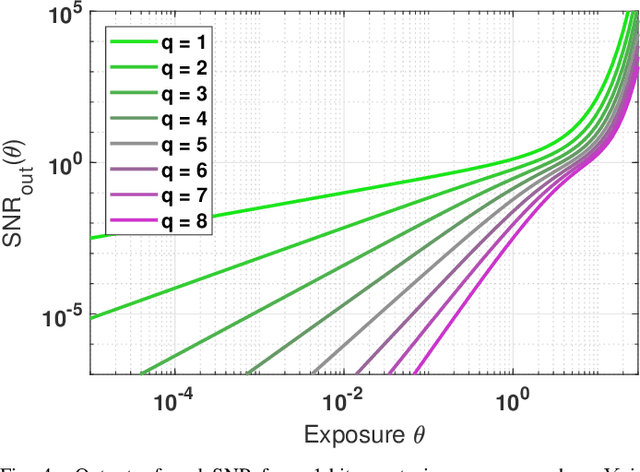
The signal-to-noise ratio (SNR) of a digital image sensor is typically defined as the ratio between the mean over the standard deviation of the sensor's output, thus known as the output-referred SNR. For sensors with a large full-well capacity, the output-referred SNR demonstrates the well-known linear response in the log-log scale. However, as the input exposure approaches the full-well capacity, the vanishing randomness of the saturated pixel will cause this output-referred SNR to artificially go to infinity. Since modern digital image sensors have a small pitch and hence a small full-well capacity, the shortcomings of the output-referred SNR motivated the development of a theoretical concept known as the exposure-referred SNR, first reported in some sensors and computer vision papers in the 1990's and more since 2010. Some intuitions of the exposure-referred SNR have been discussed in the past, but little is known how the exposure-referred SNR can be rigorously derived. Recognizing the significance of such an analysis to all present and future small pixels, this paper presents a theoretical analysis to justify the definition and answer four questions: (1) What is the correct definition of SNR? (2) How is the output-referred SNR related to the exposure-referred SNR? (3) For simple noise models, the SNRs can be analytically derived, but for complex noise models, how to numerically compute the SNR? (4) What utilities can the exposure-referred SNR bring to solving imaging tasks? New theoretical results are shown to confirm the validity of the exposure-referred SNR for image sensors of any bit-depth and full-well capacity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge