Exploring Strategy-Proofness, Uniqueness, and Pareto Optimality for the Stable Matching Problem with Couples
Paper and Code
May 13, 2015
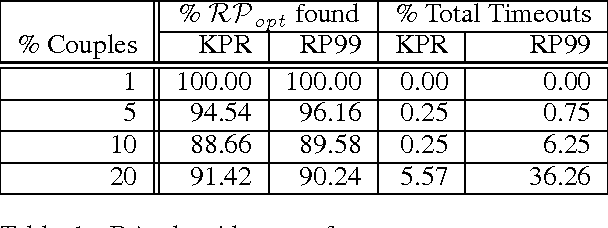

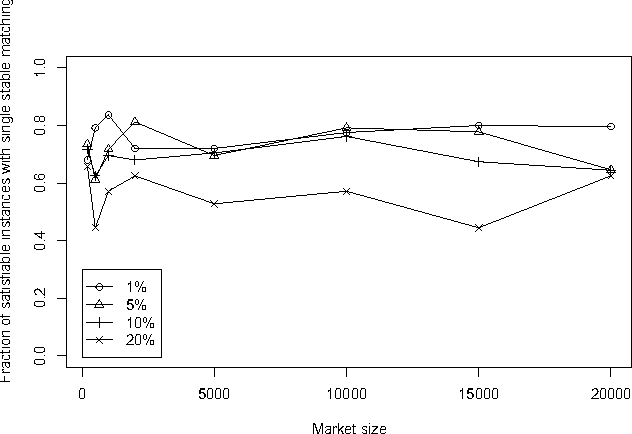
The Stable Matching Problem with Couples (SMP-C) is a ubiquitous real-world extension of the stable matching problem (SMP) involving complementarities. Although SMP can be solved in polynomial time, SMP-C is NP-Complete. Hence, it is not clear which, if any, of the theoretical results surrounding the canonical SMP problem apply in this setting. In this paper, we use a recently-developed SAT encoding to solve SMP-C exactly. This allows us to enumerate all stable matchings for any given instance of SMP-C. With this tool, we empirically evaluate some of the properties that have been hypothesized to hold for SMP-C. We take particular interest in investigating if, as the size of the market grows, the percentage of instances with unique stable matchings also grows. While we did not find this trend among the random problem instances we sampled, we did find that the percentage of instances with an resident optimal matching seems to more closely follow the trends predicted by previous conjectures. We also define and investigate resident Pareto optimal stable matchings, finding that, even though this is important desideratum for the deferred acceptance style algorithms previously designed to solve SMP-C, they do not always find one. We also investigate strategy-proofness for SMP-C, showing that even if only one stable matching exists, residents still have incentive to misreport their preferences. However, if a problem has a resident optimal stable matching, we show that residents cannot manipulate via truncation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge