Exploring Rawlsian Fairness for K-Means Clustering
Paper and Code
May 04, 2022
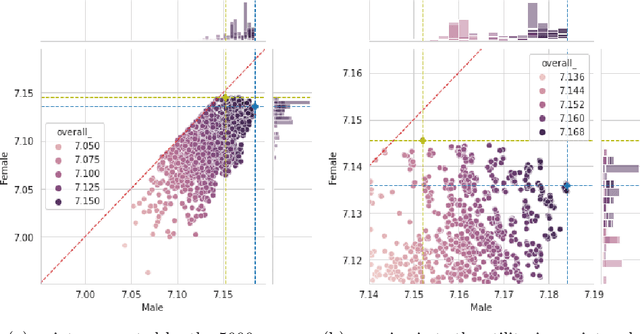
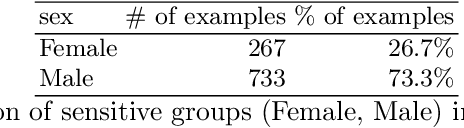
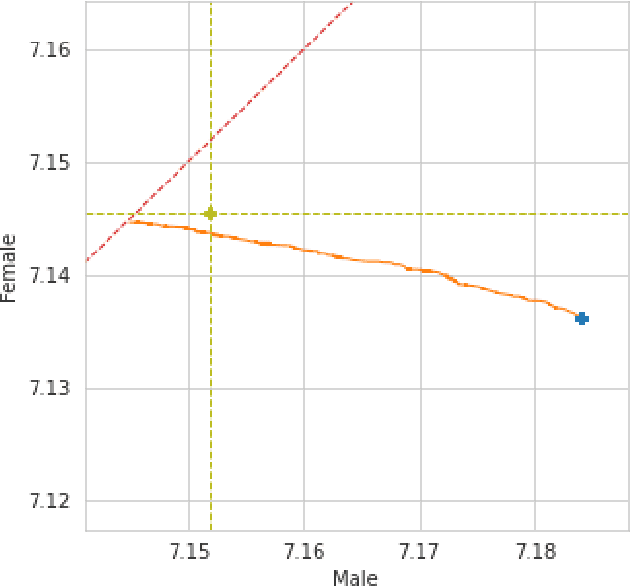
We conduct an exploratory study that looks at incorporating John Rawls' ideas on fairness into existing unsupervised machine learning algorithms. Our focus is on the task of clustering, specifically the k-means clustering algorithm. To the best of our knowledge, this is the first work that uses Rawlsian ideas in clustering. Towards this, we attempt to develop a postprocessing technique i.e., one that operates on the cluster assignment generated by the standard k-means clustering algorithm. Our technique perturbs this assignment over a number of iterations to make it fairer according to Rawls' difference principle while minimally affecting the overall utility. As the first step, we consider two simple perturbation operators -- $\mathbf{R_1}$ and $\mathbf{R_2}$ -- that reassign examples in a given cluster assignment to new clusters; $\mathbf{R_1}$ assigning a single example to a new cluster, and $\mathbf{R_2}$ a pair of examples to new clusters. Our experiments on a sample of the Adult dataset demonstrate that both operators make meaningful perturbations in the cluster assignment towards incorporating Rawls' difference principle, with $\mathbf{R_2}$ being more efficient than $\mathbf{R_1}$ in terms of the number of iterations. However, we observe that there is still a need to design operators that make significantly better perturbations. Nevertheless, both operators provide good baselines for designing and comparing any future operator, and we hope our findings would aid future work in this direction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge