Exploring Group and Symmetry Principles in Large Language Models
Paper and Code
Feb 09, 2024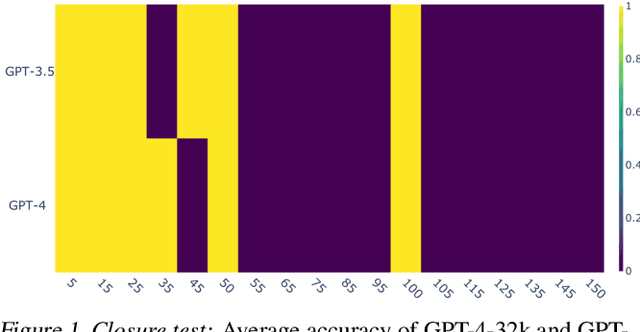
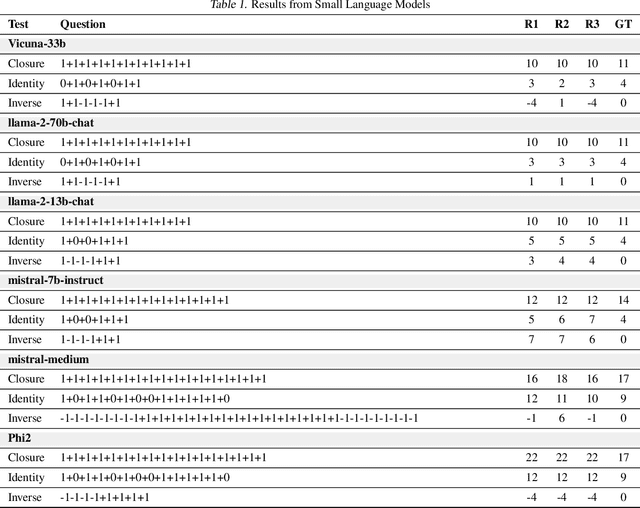
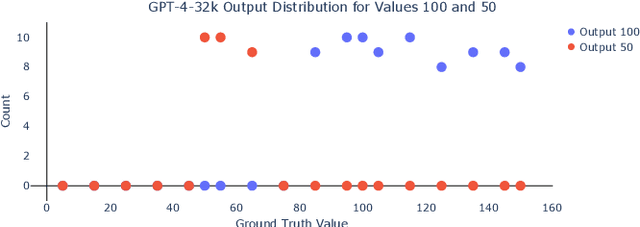
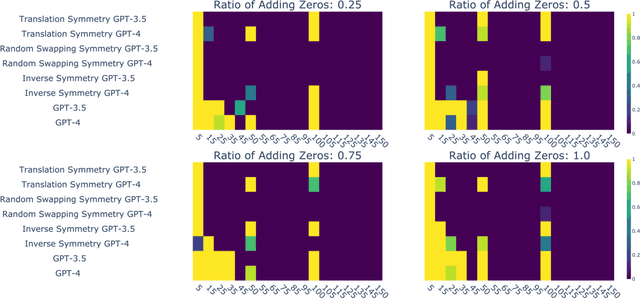
Large Language Models (LLMs) have demonstrated impressive performance across a wide range of applications; however, assessing their reasoning capabilities remains a significant challenge. In this paper, we introduce a framework grounded in group and symmetry principles, which have played a crucial role in fields such as physics and mathematics, and offer another way to evaluate their capabilities. While the proposed framework is general, to showcase the benefits of employing these properties, we focus on arithmetic reasoning and investigate the performance of these models on four group properties: closure, identity, inverse, and associativity. Our findings reveal that LLMs studied in this work struggle to preserve group properties across different test regimes. In the closure test, we observe biases towards specific outputs and an abrupt degradation in their performance from 100% to 0% after a specific sequence length. They also perform poorly in the identity test, which represents adding irrelevant information in the context, and show sensitivity when subjected to inverse test, which examines the robustness of the model with respect to negation. In addition, we demonstrate that breaking down problems into smaller steps helps LLMs in the associativity test that we have conducted. To support these tests we have developed a synthetic dataset which will be released.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge