Exploiting Structure of Uncertainty for Efficient Combinatorial Semi-Bandits

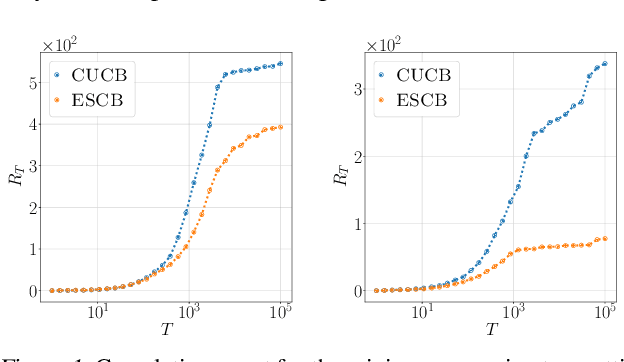
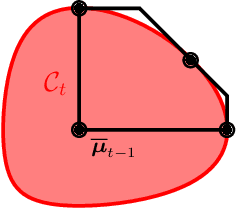
We improve the efficiency of algorithms for stochastic \emph{combinatorial semi-bandits}. In most interesting problems, state-of-the-art algorithms take advantage of structural properties of rewards, such as \emph{independence}. However, while being minimax optimal in terms of regret, these algorithms are intractable. In our paper, we first reduce their implementation to a specific \emph{submodular maximization}. Then, in case of \emph{matroid} constraints, we design adapted approximation routines, thereby providing the first efficient algorithms that exploit the reward structure. In particular, we improve the state-of-the-art efficient gap-free regret bound by a factor $\sqrt{k}$, where $k$ is the maximum action size. Finally, we show how our improvement translates to more general \emph{budgeted combinatorial semi-bandits}.