Exploiting Restricted Boltzmann Machines and Deep Belief Networks in Compressed Sensing
Paper and Code
May 30, 2017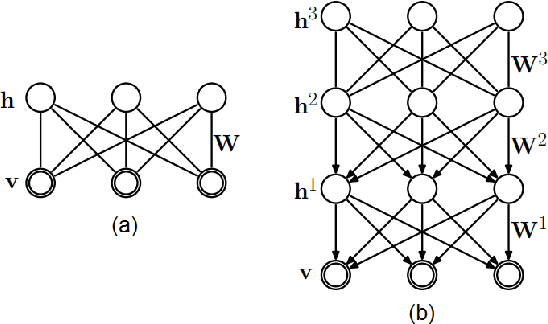
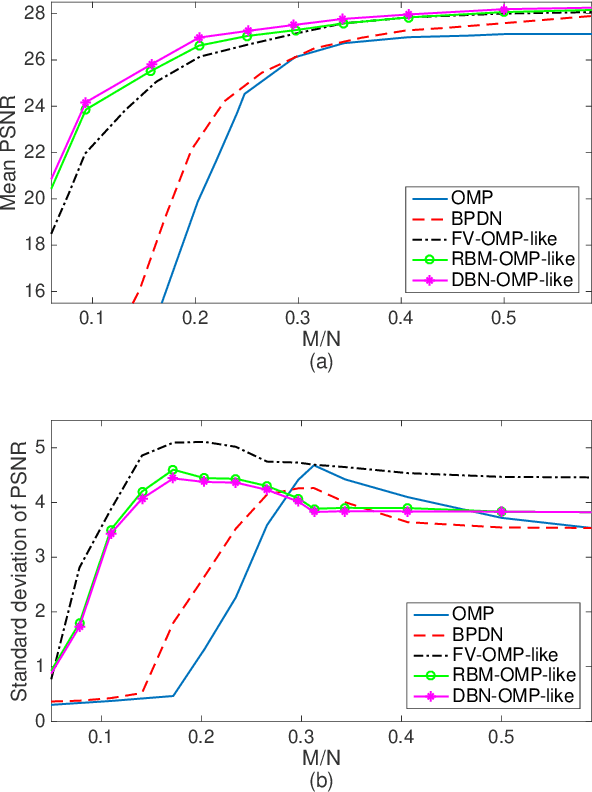

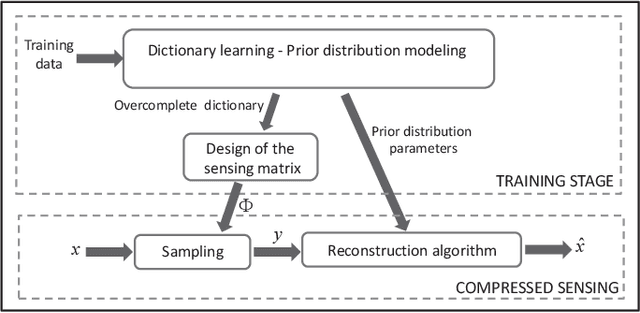
This paper proposes a CS scheme that exploits the representational power of restricted Boltzmann machines and deep learning architectures to model the prior distribution of the sparsity pattern of signals belonging to the same class. The determined probability distribution is then used in a maximum a posteriori (MAP) approach for the reconstruction. The parameters of the prior distribution are learned from training data. The motivation behind this approach is to model the higher-order statistical dependencies between the coefficients of the sparse representation, with the final goal of improving the reconstruction. The performance of the proposed method is validated on the Berkeley Segmentation Dataset and the MNIST Database of handwritten digits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge