Explicit homography estimation improves contrastive self-supervised learning
Paper and Code
Jan 12, 2021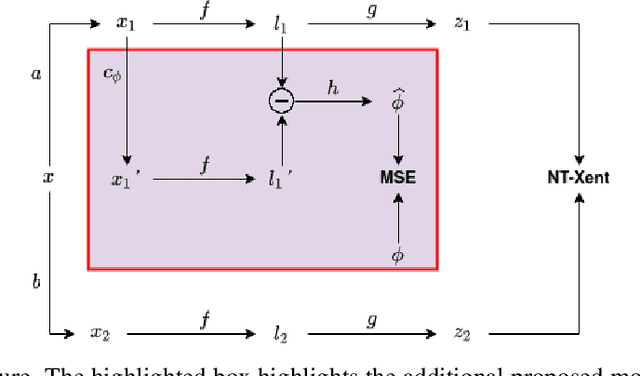

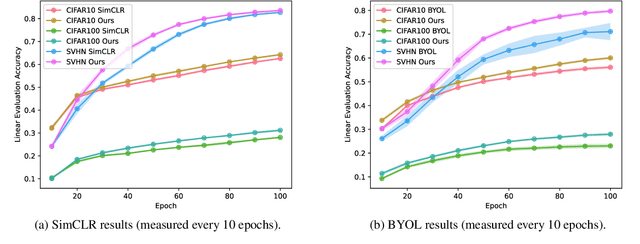
The typical contrastive self-supervised algorithm uses a similarity measure in latent space as the supervision signal by contrasting positive and negative images directly or indirectly. Although the utility of self-supervised algorithms has improved recently, there are still bottlenecks hindering their widespread use, such as the compute needed. In this paper, we propose a module that serves as an additional objective in the self-supervised contrastive learning paradigm. We show how the inclusion of this module to regress the parameters of an affine transformation or homography, in addition to the original contrastive objective, improves both performance and learning speed. Importantly, we ensure that this module does not enforce invariance to the various components of the affine transform, as this is not always ideal. We demonstrate the effectiveness of the additional objective on two recent, popular self-supervised algorithms. We perform an extensive experimental analysis of the proposed method and show an improvement in performance for all considered datasets. Further, we find that although both the general homography and affine transformation are sufficient to improve performance and convergence, the affine transformation performs better in all cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge