Expectation Propogation for approximate inference in dynamic Bayesian networks

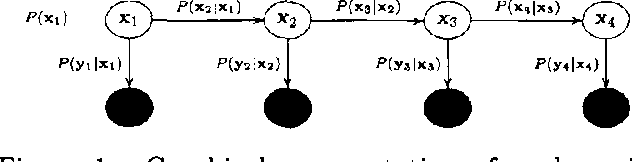
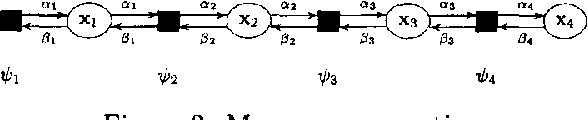
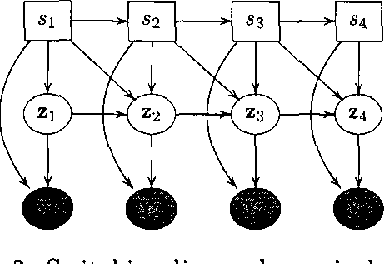
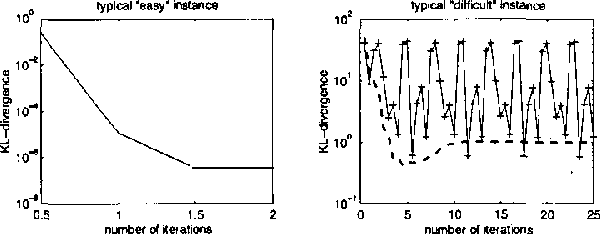
We describe expectation propagation for approximate inference in dynamic Bayesian networks as a natural extension of Pearl s exact belief propagation.Expectation propagation IS a greedy algorithm, converges IN many practical cases, but NOT always.We derive a DOUBLE - loop algorithm, guaranteed TO converge TO a local minimum OF a Bethe free energy.Furthermore, we show that stable fixed points OF (damped) expectation propagation correspond TO local minima OF this free energy, but that the converse need NOT be the CASE .We illustrate the algorithms BY applying them TO switching linear dynamical systems AND discuss implications FOR approximate inference IN general Bayesian networks.