Exactly Robust Kernel Principal Component Analysis

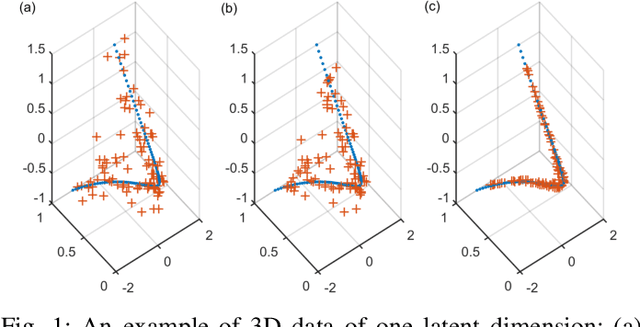
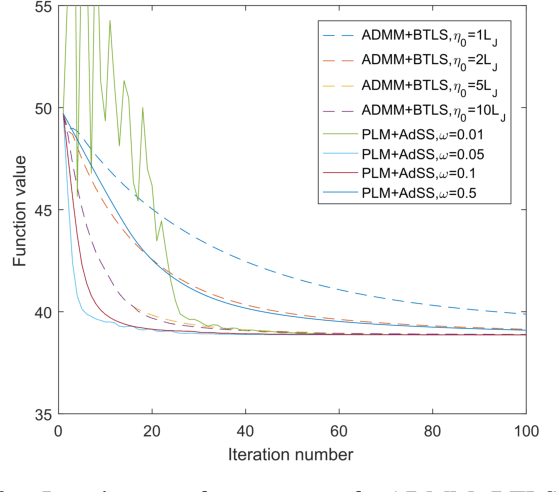
We propose a novel method called robust kernel principal component analysis (RKPCA) to decompose a partially corrupted matrix as a sparse matrix plus a high or full-rank matrix whose columns are drawn from a nonlinear low-dimensional latent variable model. RKPCA can be applied to many problems such as noise removal and subspace clustering and is so far the only unsupervised nonlinear method robust to sparse noises. We also provide theoretical guarantees for RKPCA. The optimization of RKPCA is challenging because it involves nonconvex and indifferentiable problems simultaneously. We propose two nonconvex optimization algorithms for RKPCA: alternating direction method of multipliers with backtracking line search and proximal linearized minimization with adaptive step size. Comparative studies on synthetic data and nature images corroborate the effectiveness and superiority of RKPCA in noise removal and robust subspace clustering.