Exact Reconstruction of the Rank Order Coding using Frames Theory

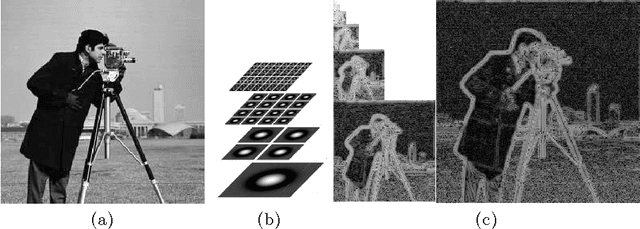
Our goal is to revisit rank order coding by proposing an original exact decoding procedure for it. Rank order coding was proposed by Simon Thorpe et al. who stated that the retina represents the visual stimulus by the order in which its cells are activated. A classical rank order coder/decoder was then designed on this basis [1]. Though, it appeared that the decoding procedure employed yields reconstruction errors that limit the model Rate/Quality performances when used as an image codec. The attempts made in the literature to overcome this issue are time consuming and alter the coding procedure, or are lacking mathematical support and feasibility for standard size images. Here we solve this problem in an original fashion by using the frames theory, where a frame of a vector space designates an extension for the notion of basis. First, we prove that the analyzing filter bank considered is a frame, and then we define the corresponding dual frame that is necessary for the exact image reconstruction. Second, to deal with the problem of memory overhead, we design a recursive out-of-core blockwise algorithm for the computation of this dual frame. Our work provides a mathematical formalism for the retinal model under study and defines a simple and exact reverse transform for it with up to 270 dB of PSNR gain compared to [1]. Furthermore, the framework presented here can be extended to several models of the visual cortical areas using redundant representations.