Exact Optimization of Conformal Predictors via Incremental and Decremental Learning
Paper and Code
Feb 05, 2021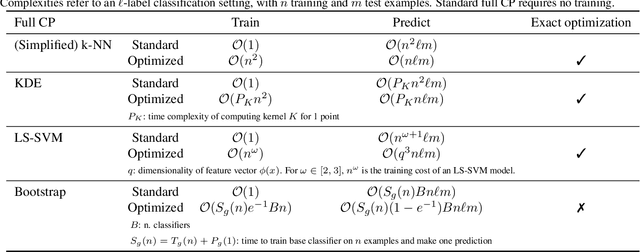
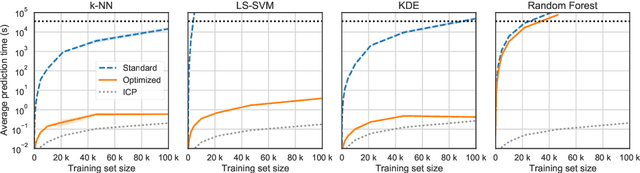
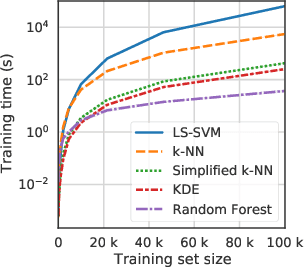
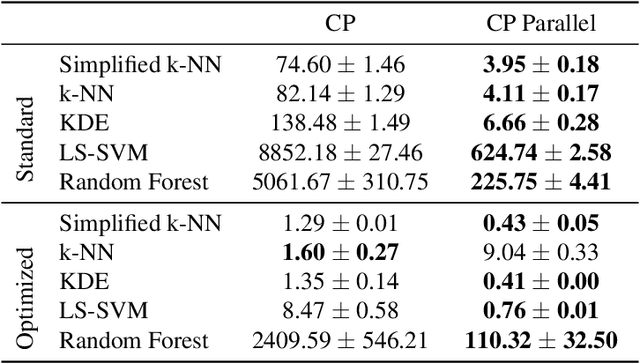
Conformal Predictors (CP) are wrappers around ML methods, providing error guarantees under weak assumptions on the data distribution. They are suitable for a wide range of problems, from classification and regression to anomaly detection. Unfortunately, their high computational complexity limits their applicability to large datasets. In this work, we show that it is possible to speed up a CP classifier considerably, by studying it in conjunction with the underlying ML method, and by exploiting incremental&decremental learning. For methods such as k-NN, KDE, and kernel LS-SVM, our approach reduces the running time by one order of magnitude, whilst producing exact solutions. With similar ideas, we also achieve a linear speed up for the harder case of bootstrapping. Finally, we extend these techniques to improve upon an optimization of k-NN CP for regression. We evaluate our findings empirically, and discuss when methods are suitable for CP optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge