Exact information propagation through fully-connected feed forward neural networks

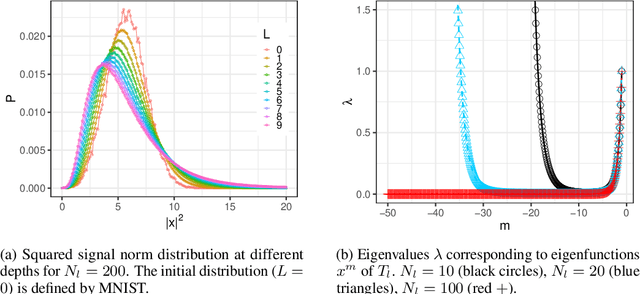
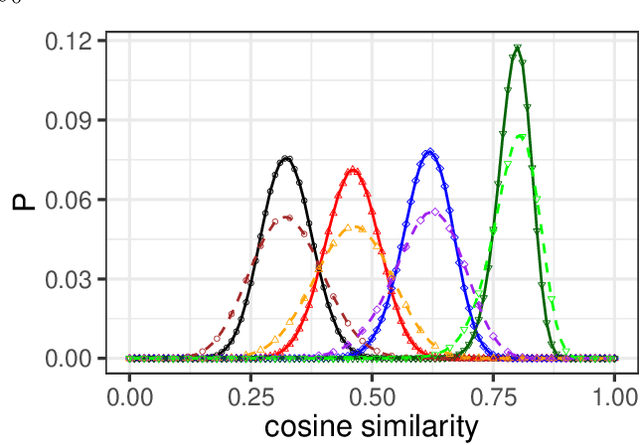
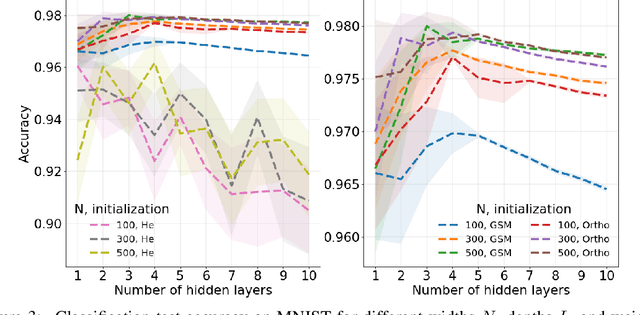
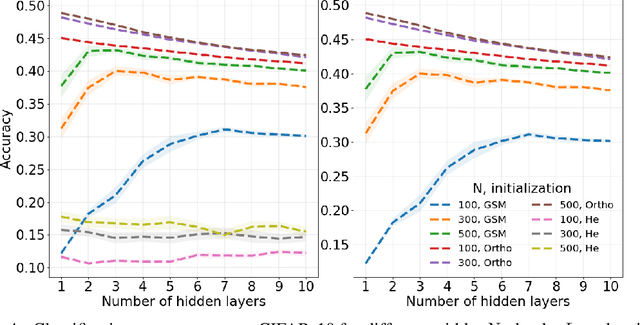
Neural network ensembles at initialisation give rise to the trainability and training speed of neural networks and thus support parameter choices at initialisation. These insights rely so far on mean field approximations that assume infinite layer width and study average squared signals. Thus, information about the full output distribution gets lost. Therefore, we derive the output distribution exactly (without mean field assumptions), for fully-connected networks with Gaussian weights and biases. The layer-wise transition of the signal distribution is guided by a linear integral operator, whose kernel has a closed form solution in case of rectified linear units for nonlinear activations. This enables us to analyze some of its spectral properties, for instance, the shape of the stationary distribution for different parameter choices and the dynamics of signal propagation.