Evolutionary n-level Hypergraph Partitioning with Adaptive Coarsening
Paper and Code
Oct 08, 2018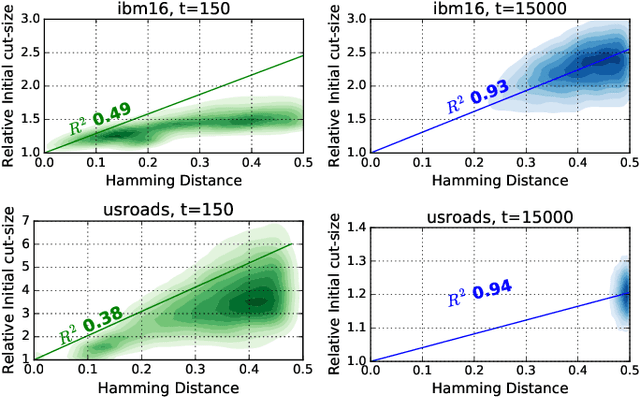
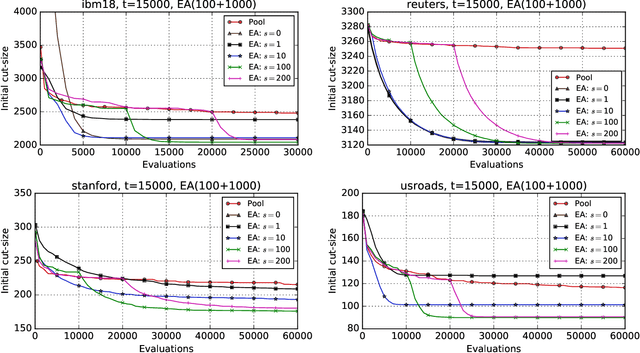
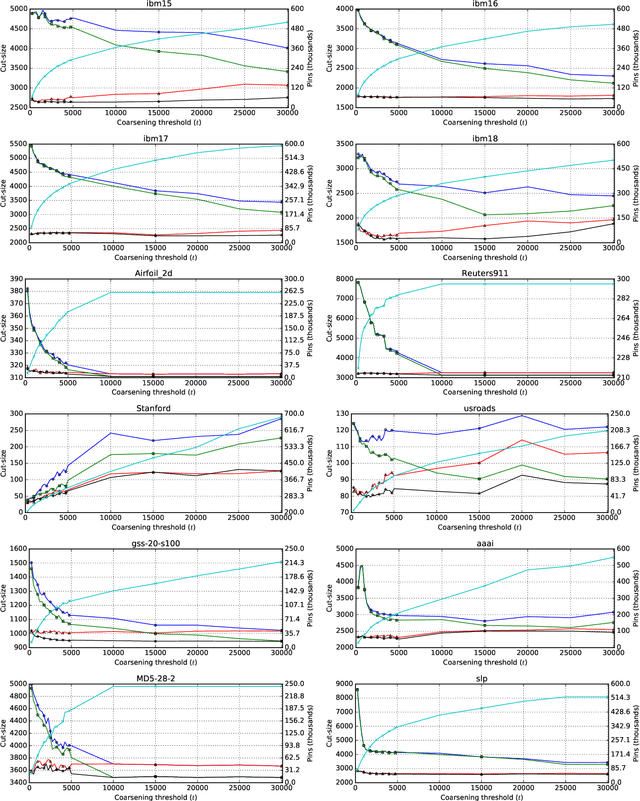
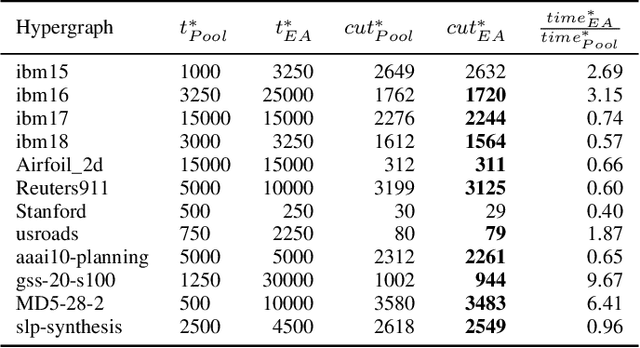
Hypergraph partitioning is an NP-hard problem that occurs in many computer science applications where it is necessary to reduce large problems into a number of smaller, computationally tractable sub-problems. Current techniques use a multilevel approach wherein an initial partitioning is performed after compressing the hypergraph to a predetermined level. This level is typically chosen to produce very coarse hypergraphs in which heuristic algorithms are fast and effective. This article presents a novel memetic algorithm which remains effective on larger initial hypergraphs. This enables the exploitation of information that can be lost during coarsening and results in improved final solution quality. We use this algorithm to present an empirical analysis of the space of possible initial hypergraphs in terms of its searchability at different levels of coarsening. We find that the best results arise at coarsening levels unique to each hypergraph. Based on this, we introduce an adaptive scheme that stops coarsening when the rate of information loss in a hypergraph becomes non-linear and show that this produces further improvements. The results show that we have identified a valuable role for evolutionary algorithms within the current state-of-the-art hypergraph partitioning framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge