Evaluating Robustness of Neural Networks with Mixed Integer Programming
Paper and Code
Jun 11, 2018


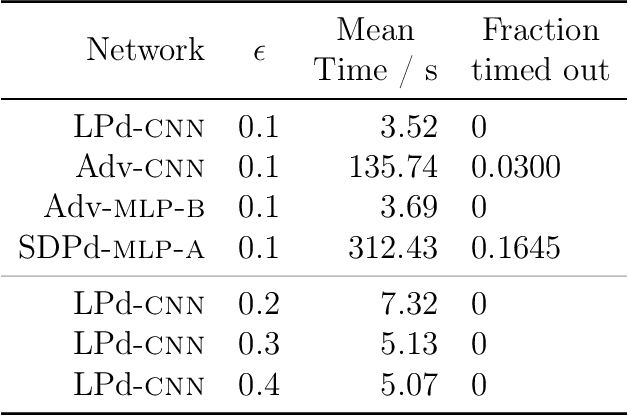
Neural networks have demonstrated considerable success on a wide variety of real-world problems. However, networks trained only to optimize for training accuracy can often be fooled by adversarial examples - slightly perturbed inputs that are misclassified with high confidence. Verification of networks enables us to gauge their vulnerability to such adversarial examples. We formulate verification of piecewise-linear neural networks as a mixed integer program. On a representative task of finding minimum adversarial distortions, our verifier is two to three orders of magnitude quicker than the state-of-the-art. We achieve this computational speedup via tight formulations for non-linearities, as well as a novel presolve algorithm that makes full use of all information available. The computational speedup allows us to verify properties on convolutional networks with an order of magnitude more ReLUs than networks previously verified by any complete verifier. In particular, we determine for the first time the exact adversarial accuracy of an MNIST classifier to perturbations with bounded $l_\infty$ norm $\epsilon=0.1$: for this classifier, we find an adversarial example for 4.38% of samples, and a certificate of robustness (to perturbations with bounded norm) for the remainder. Across all robust training procedures and network architectures considered, we are able to certify more samples than the state-of-the-art and find more adversarial examples than a strong first-order attack.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge