Evaluating Relaxations of Logic for Neural Networks: A Comprehensive Study
Paper and Code
Jul 28, 2021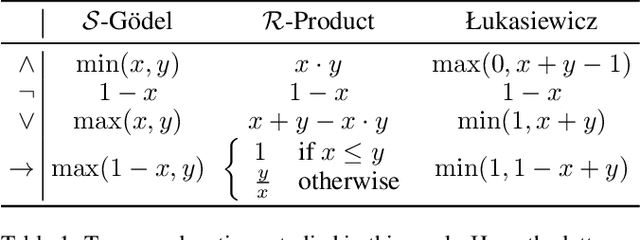
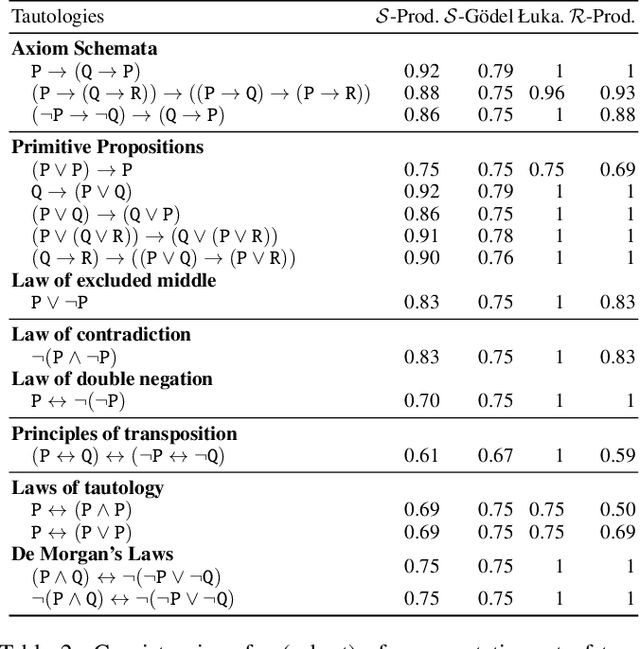

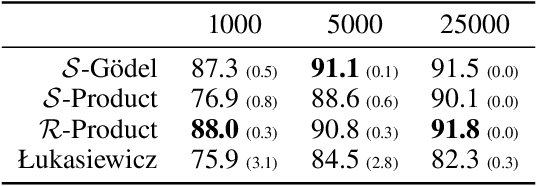
Symbolic knowledge can provide crucial inductive bias for training neural models, especially in low data regimes. A successful strategy for incorporating such knowledge involves relaxing logical statements into sub-differentiable losses for optimization. In this paper, we study the question of how best to relax logical expressions that represent labeled examples and knowledge about a problem; we focus on sub-differentiable t-norm relaxations of logic. We present theoretical and empirical criteria for characterizing which relaxation would perform best in various scenarios. In our theoretical study driven by the goal of preserving tautologies, the Lukasiewicz t-norm performs best. However, in our empirical analysis on the text chunking and digit recognition tasks, the product t-norm achieves best predictive performance. We analyze this apparent discrepancy, and conclude with a list of best practices for defining loss functions via logic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge