Evaluating Lottery Tickets Under Distributional Shifts
Paper and Code
Oct 28, 2019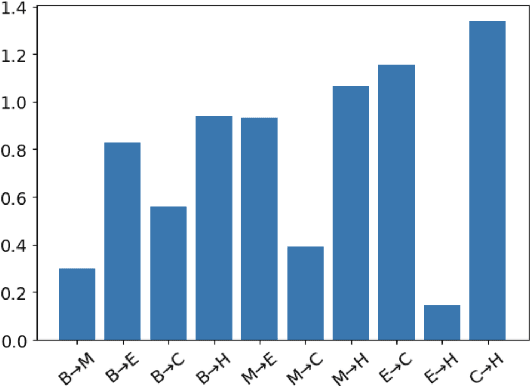
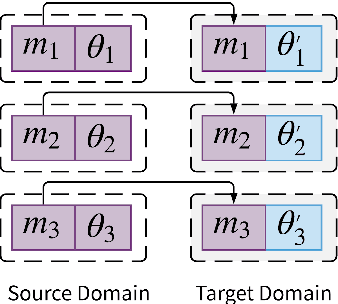
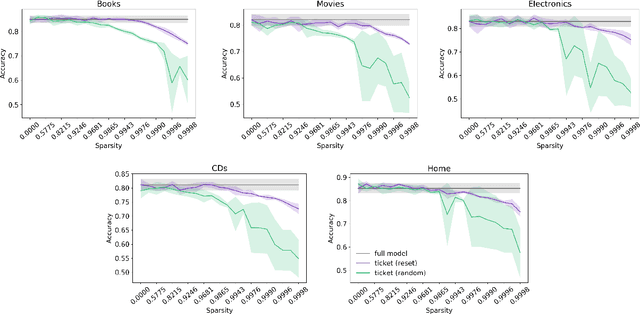
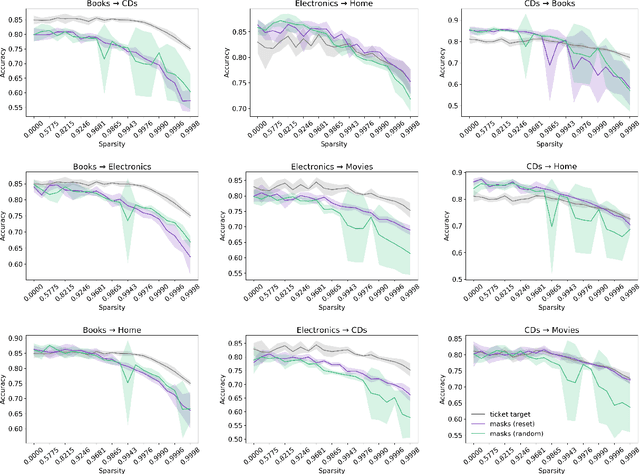
The Lottery Ticket Hypothesis suggests large, over-parameterized neural networks consist of small, sparse subnetworks that can be trained in isolation to reach a similar (or better) test accuracy. However, the initialization and generalizability of the obtained sparse subnetworks have been recently called into question. Our work focuses on evaluating the initialization of sparse subnetworks under distributional shifts. Specifically, we investigate the extent to which a sparse subnetwork obtained in a source domain can be re-trained in isolation in a dissimilar, target domain. In addition, we examine the effects of different initialization strategies at transfer-time. Our experiments show that sparse subnetworks obtained through lottery ticket training do not simply overfit to particular domains, but rather reflect an inductive bias of deep neural networks that can be exploited in multiple domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge