Estimation of Bandlimited Grayscale Images From the Single Bit Observations of Pixels Affected by Additive Gaussian Noise
Paper and Code
Oct 27, 2016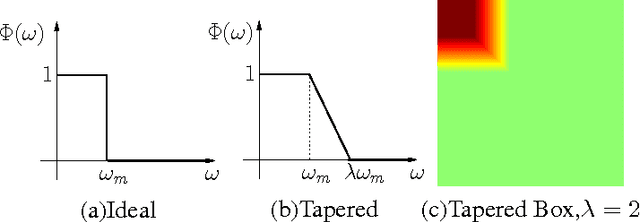
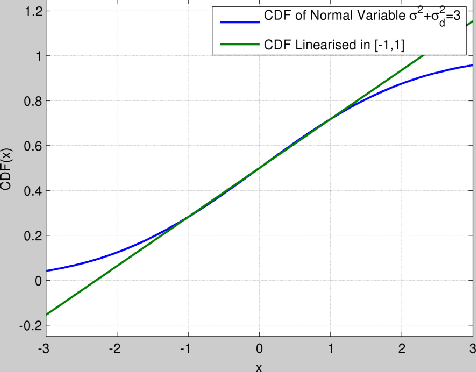
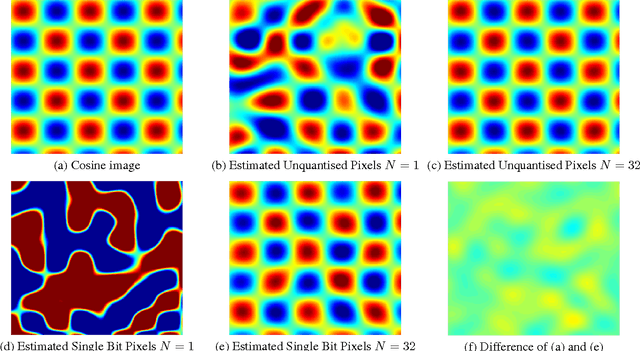

The estimation of grayscale images using their single-bit zero mean Gaussian noise-affected pixels is presented in this paper. The images are assumed to be bandlimited in the Fourier Cosine transform (FCT) domain. The images are oversampled over their Nyquist rate in the FCT domain. We propose a non-recursive approach based on first order approximation of Cumulative Distribution Function (CDF) to estimate the image from single bit pixels which itself is based on Banach's contraction theorem. The decay rate for mean squared error of estimating such images is found to be independent of the precision of the quantizer and it varies as $O(1/N)$ where $N$ is the "effective" oversampling ratio with respect to the Nyquist rate in the FCT domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge