Estimation in Rotationally Invariant Generalized Linear Models via Approximate Message Passing
Paper and Code
Dec 08, 2021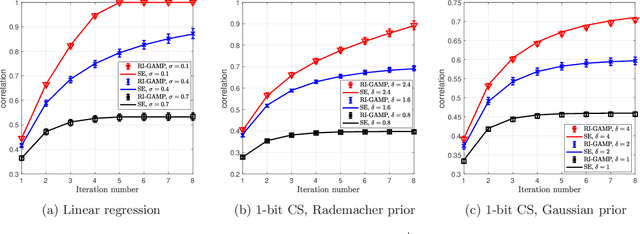
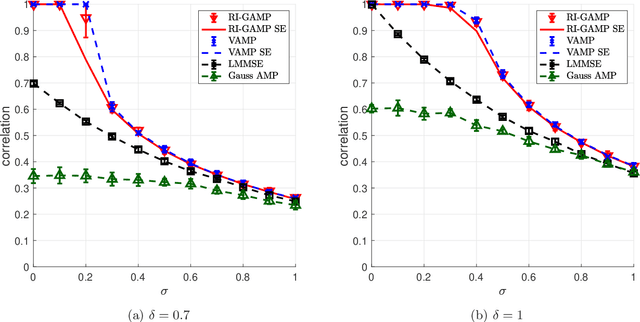
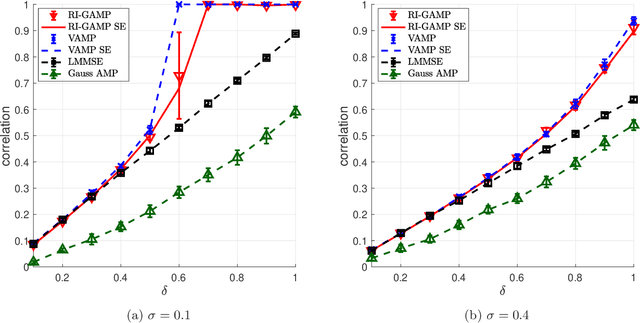
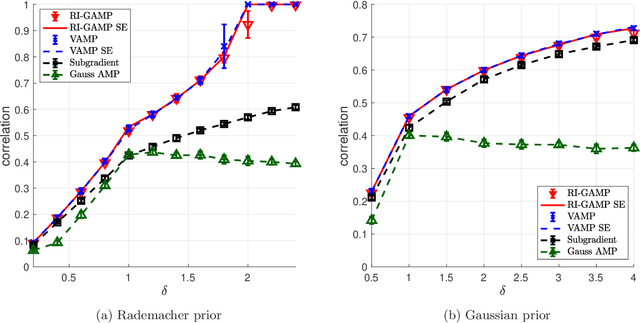
We consider the problem of signal estimation in generalized linear models defined via rotationally invariant design matrices. Since these matrices can have an arbitrary spectral distribution, this model is well suited to capture complex correlation structures which often arise in applications. We propose a novel family of approximate message passing (AMP) algorithms for signal estimation, and rigorously characterize their performance in the high-dimensional limit via a state evolution recursion. Assuming knowledge of the design matrix spectrum, our rotationally invariant AMP has complexity of the same order as the existing AMP for Gaussian matrices; it also recovers the existing AMP as a special case. Numerical results showcase a performance close to Vector AMP (which is conjectured to be Bayes-optimal in some settings), but obtained with a much lower complexity, as the proposed algorithm does not require a computationally expensive singular value decomposition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge