Estimation and Inference for Causal Functions with Multiway Clustered Data
Paper and Code
Sep 10, 2024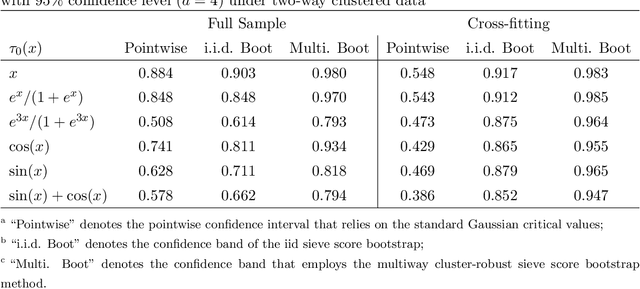
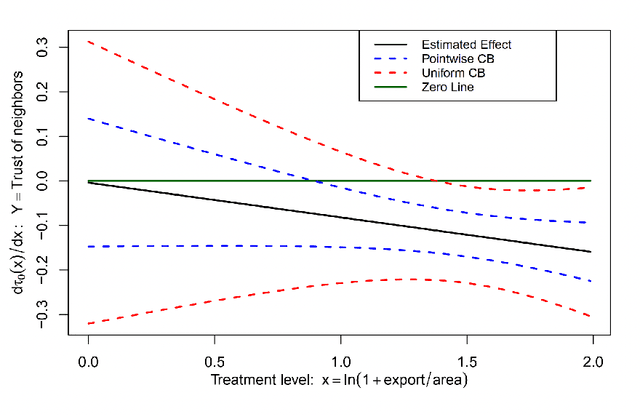
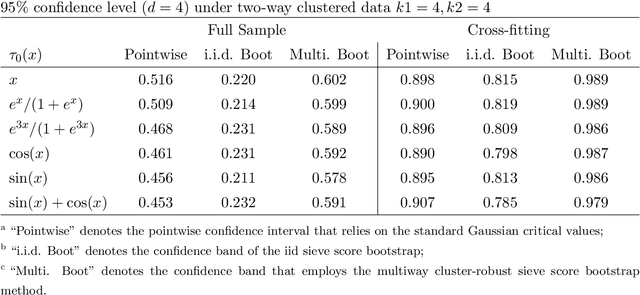
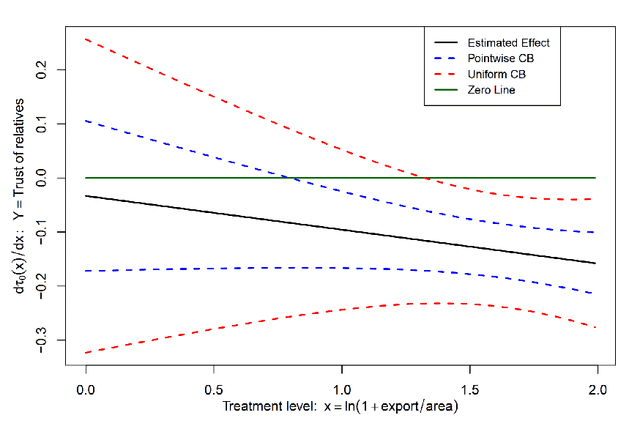
This paper proposes methods of estimation and uniform inference for a general class of causal functions, such as the conditional average treatment effects and the continuous treatment effects, under multiway clustering. The causal function is identified as a conditional expectation of an adjusted (Neyman-orthogonal) signal that depends on high-dimensional nuisance parameters. We propose a two-step procedure where the first step uses machine learning to estimate the high-dimensional nuisance parameters. The second step projects the estimated Neyman-orthogonal signal onto a dictionary of basis functions whose dimension grows with the sample size. For this two-step procedure, we propose both the full-sample and the multiway cross-fitting estimation approaches. A functional limit theory is derived for these estimators. To construct the uniform confidence bands, we develop a novel resampling procedure, called the multiway cluster-robust sieve score bootstrap, that extends the sieve score bootstrap (Chen and Christensen, 2018) to the novel setting with multiway clustering. Extensive numerical simulations showcase that our methods achieve desirable finite-sample behaviors. We apply the proposed methods to analyze the causal relationship between mistrust levels in Africa and the historical slave trade. Our analysis rejects the null hypothesis of uniformly zero effects and reveals heterogeneous treatment effects, with significant impacts at higher levels of trade volumes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge