Estimating the Fundamental Limits is Easier than Achieving the Fundamental Limits
Paper and Code
Oct 01, 2017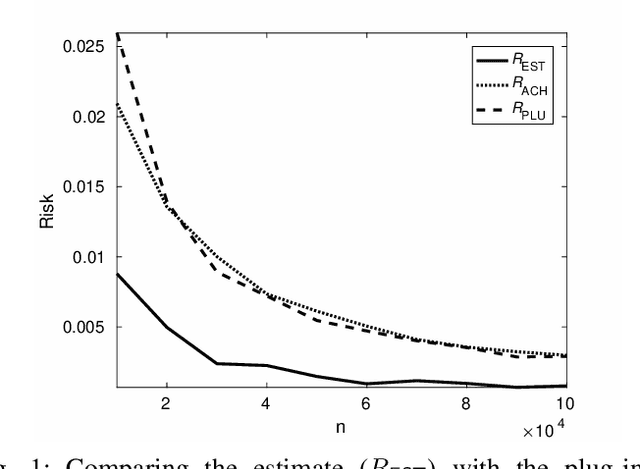
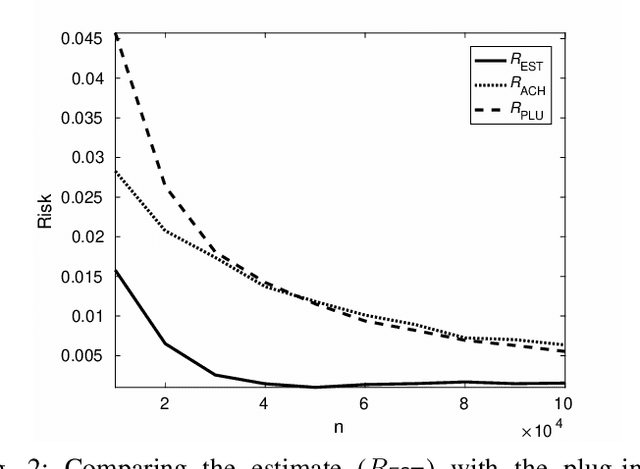
We show through case studies that it is easier to estimate the fundamental limits of data processing than to construct explicit algorithms to achieve those limits. Focusing on binary classification, data compression, and prediction under logarithmic loss, we show that in the finite space setting, when it is possible to construct an estimator of the limits with vanishing error with $n$ samples, it may require at least $n\ln n$ samples to construct an explicit algorithm to achieve the limits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge