Estimating the Completeness of Discrete Speech Units
Paper and Code
Sep 09, 2024
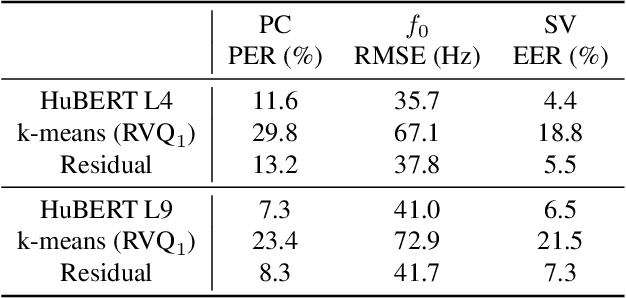

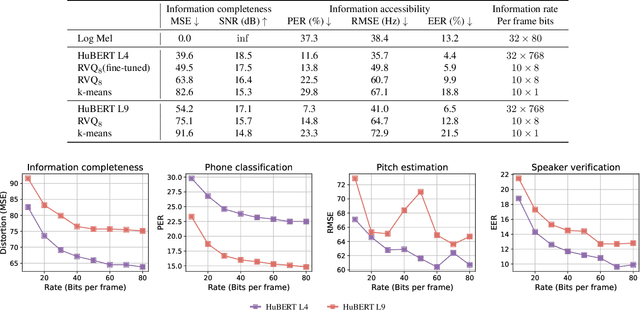
Representing speech with discrete units has been widely used in speech codec and speech generation. However, there are several unverified claims about self-supervised discrete units, such as disentangling phonetic and speaker information with k-means, or assuming information loss after k-means. In this work, we take an information-theoretic perspective to answer how much information is present (information completeness) and how much information is accessible (information accessibility), before and after residual vector quantization. We show a lower bound for information completeness and estimate completeness on discretized HuBERT representations after residual vector quantization. We find that speaker information is sufficiently present in HuBERT discrete units, and that phonetic information is sufficiently present in the residual, showing that vector quantization does not achieve disentanglement. Our results offer a comprehensive assessment on the choice of discrete units, and suggest that a lot more information in the residual should be mined rather than discarded.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge