Estimating $α$-Rank by Maximizing Information Gain
Paper and Code
Jan 22, 2021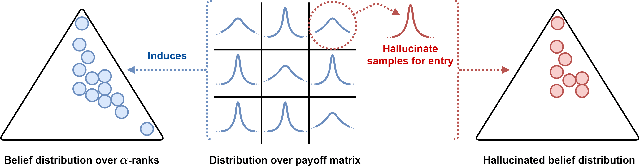
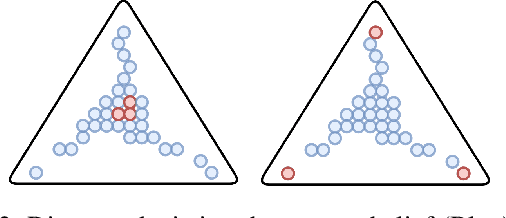
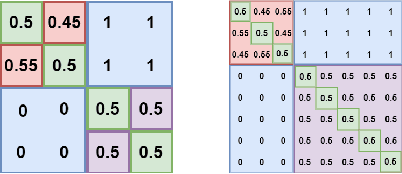
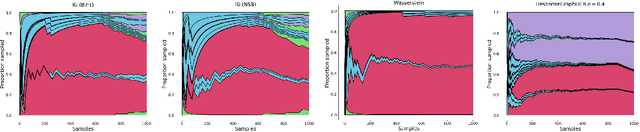
Game theory has been increasingly applied in settings where the game is not known outright, but has to be estimated by sampling. For example, meta-games that arise in multi-agent evaluation can only be accessed by running a succession of expensive experiments that may involve simultaneous deployment of several agents. In this paper, we focus on $\alpha$-rank, a popular game-theoretic solution concept designed to perform well in such scenarios. We aim to estimate the $\alpha$-rank of the game using as few samples as possible. Our algorithm maximizes information gain between an epistemic belief over the $\alpha$-ranks and the observed payoff. This approach has two main benefits. First, it allows us to focus our sampling on the entries that matter the most for identifying the $\alpha$-rank. Second, the Bayesian formulation provides a facility to build in modeling assumptions by using a prior over game payoffs. We show the benefits of using information gain as compared to the confidence interval criterion of ResponseGraphUCB (Rowland et al. 2019), and provide theoretical results justifying our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge