Estimating Numbers without Regression
Paper and Code
Oct 09, 2023
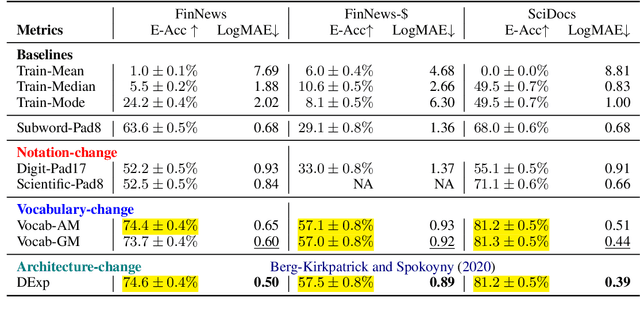
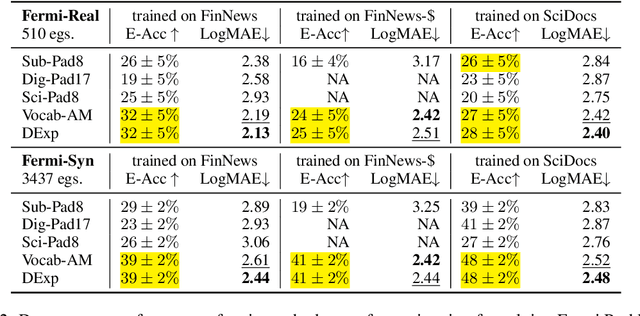
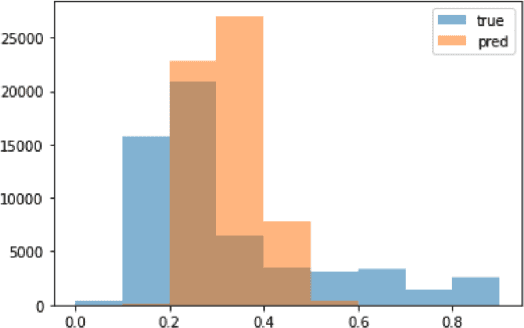
Despite recent successes in language models, their ability to represent numbers is insufficient. Humans conceptualize numbers based on their magnitudes, effectively projecting them on a number line; whereas subword tokenization fails to explicitly capture magnitude by splitting numbers into arbitrary chunks. To alleviate this shortcoming, alternative approaches have been proposed that modify numbers at various stages of the language modeling pipeline. These methods change either the (1) notation in which numbers are written (\eg scientific vs decimal), the (2) vocabulary used to represent numbers or the entire (3) architecture of the underlying language model, to directly regress to a desired number. Previous work suggests that architectural change helps achieve state-of-the-art on number estimation but we find an insightful ablation: changing the model's vocabulary instead (\eg introduce a new token for numbers in range 10-100) is a far better trade-off. In the context of masked number prediction, a carefully designed tokenization scheme is both the simplest to implement and sufficient, \ie with similar performance to the state-of-the-art approach that requires making significant architectural changes. Finally, we report similar trends on the downstream task of numerical fact estimation (for Fermi Problems) and discuss reasons behind our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge