Escaping Poor Local Minima in Large Scale Robust Estimation
Paper and Code
Feb 22, 2021
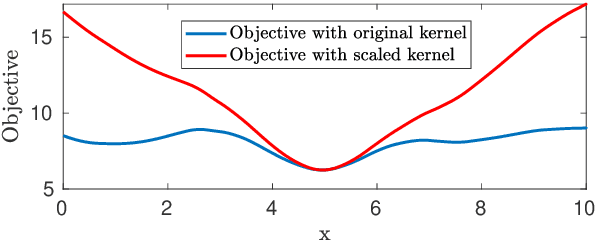
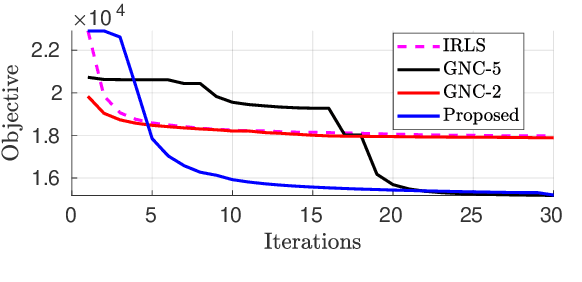
Robust parameter estimation is a crucial task in several 3D computer vision pipelines such as Structure from Motion (SfM). State-of-the-art algorithms for robust estimation, however, still suffer from difficulties in converging to satisfactory solutions due to the presence of many poor local minima or flat regions in the optimization landscapes. In this paper, we introduce two novel approaches for robust parameter estimation. The first algorithm utilizes the Filter Method (FM), which is a framework for constrained optimization allowing great flexibility in algorithmic choices, to derive an adaptive kernel scaling strategy that enjoys a strong ability to escape poor minima and achieves fast convergence rates. Our second algorithm combines a generalized Majorization Minimization (GeMM) framework with the half-quadratic lifting formulation to obtain a simple yet efficient solver for robust estimation. We empirically show that both proposed approaches show encouraging capability on avoiding poor local minima and achieve competitive results compared to existing state-of-the art robust fitting algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge