ES6D: A Computation Efficient and Symmetry-Aware 6D Pose Regression Framework
Paper and Code
Apr 03, 2022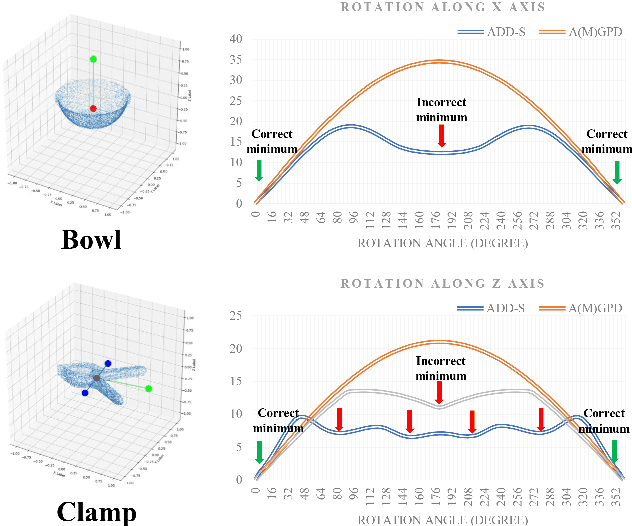

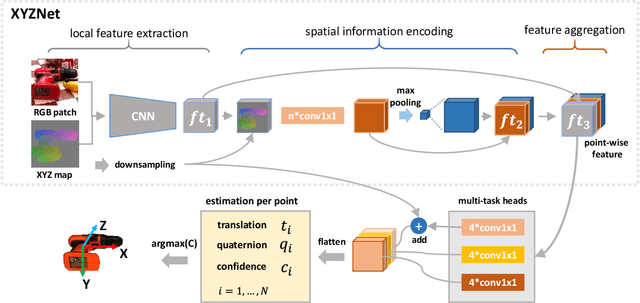

In this paper, a computation efficient regression framework is presented for estimating the 6D pose of rigid objects from a single RGB-D image, which is applicable to handling symmetric objects. This framework is designed in a simple architecture that efficiently extracts point-wise features from RGB-D data using a fully convolutional network, called XYZNet, and directly regresses the 6D pose without any post refinement. In the case of symmetric object, one object has multiple ground-truth poses, and this one-to-many relationship may lead to estimation ambiguity. In order to solve this ambiguity problem, we design a symmetry-invariant pose distance metric, called average (maximum) grouped primitives distance or A(M)GPD. The proposed A(M)GPD loss can make the regression network converge to the correct state, i.e., all minima in the A(M)GPD loss surface are mapped to the correct poses. Extensive experiments on YCB-Video and T-LESS datasets demonstrate the proposed framework's substantially superior performance in top accuracy and low computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge