ES-Based Jacobian Enables Faster Bilevel Optimization
Paper and Code
Oct 13, 2021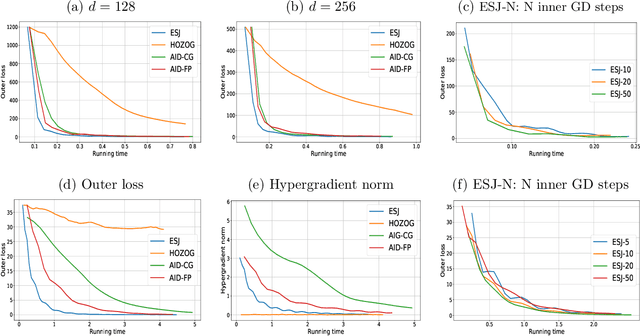


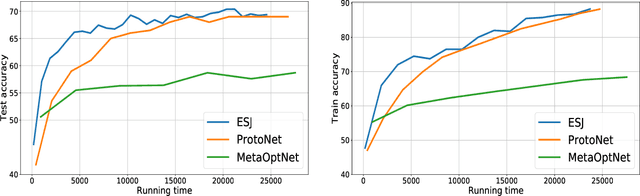
Bilevel optimization (BO) has arisen as a powerful tool for solving many modern machine learning problems. However, due to the nested structure of BO, existing gradient-based methods require second-order derivative approximations via Jacobian- or/and Hessian-vector computations, which can be very costly in practice, especially with large neural network models. In this work, we propose a novel BO algorithm, which adopts Evolution Strategies (ES) based method to approximate the response Jacobian matrix in the hypergradient of BO, and hence fully eliminates all second-order computations. We call our algorithm as ESJ (which stands for the ES-based Jacobian method) and further extend it to the stochastic setting as ESJ-S. Theoretically, we characterize the convergence guarantee and computational complexity for our algorithms. Experimentally, we demonstrate the superiority of our proposed algorithms compared to the state of the art methods on various bilevel problems. Particularly, in our experiment in the few-shot meta-learning problem, we meta-learn the twelve millions parameters of a ResNet-12 network over the miniImageNet dataset, which evidently demonstrates the scalability of our ES-based bilevel approach and its feasibility in the large-scale setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge