Equivariant Quantum Graph Circuits

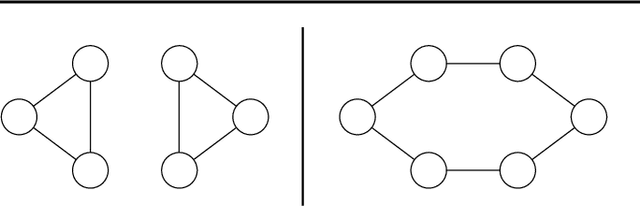
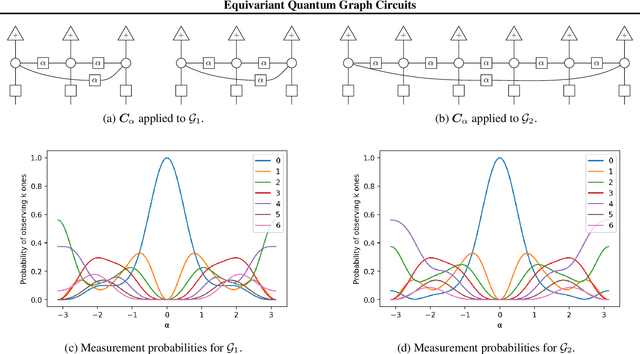
We investigate quantum circuits for graph representation learning, and propose equivariant quantum graph circuits (EQGCs), as a class of parameterized quantum circuits with strong relational inductive bias for learning over graph-structured data. Conceptually, EQGCs serve as a unifying framework for quantum graph representation learning, allowing us to define several interesting subclasses subsuming existing proposals. In terms of the representation power, we prove that the subclasses of interest are universal approximators for functions over the bounded graph domain, and provide experimental evidence. Our theoretical perspective on quantum graph machine learning methods opens many directions for further work, and could lead to models with capabilities beyond those of classical approaches.