Equivariant Disentangled Transformation for Domain Generalization under Combination Shift
Paper and Code
Aug 03, 2022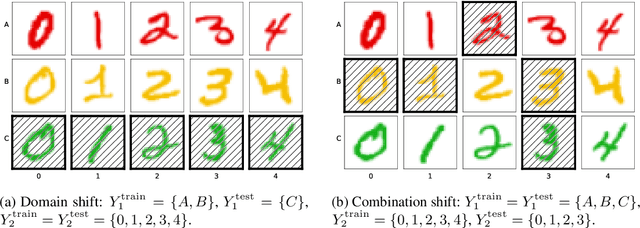
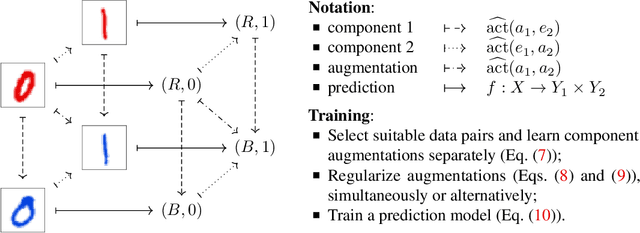
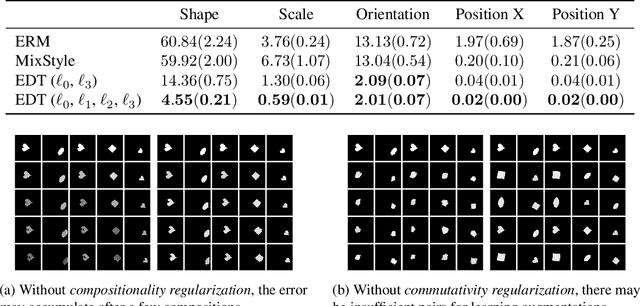
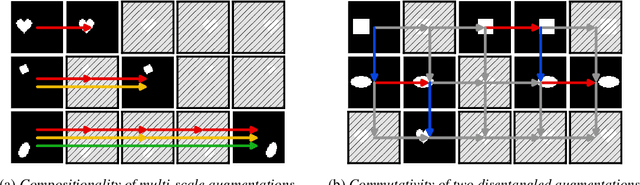
Machine learning systems may encounter unexpected problems when the data distribution changes in the deployment environment. A major reason is that certain combinations of domains and labels are not observed during training but appear in the test environment. Although various invariance-based algorithms can be applied, we find that the performance gain is often marginal. To formally analyze this issue, we provide a unique algebraic formulation of the combination shift problem based on the concepts of homomorphism, equivariance, and a refined definition of disentanglement. The algebraic requirements naturally derive a simple yet effective method, referred to as equivariant disentangled transformation (EDT), which augments the data based on the algebraic structures of labels and makes the transformation satisfy the equivariance and disentanglement requirements. Experimental results demonstrate that invariance may be insufficient, and it is important to exploit the equivariance structure in the combination shift problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge