Equal Bits: Enforcing Equally Distributed Binary Network Weights
Paper and Code
Dec 02, 2021
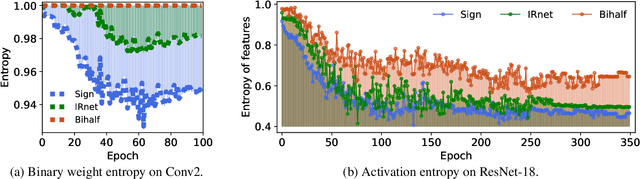

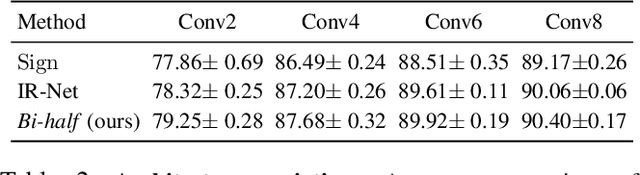
Binary networks are extremely efficient as they use only two symbols to define the network: $\{+1,-1\}$. One can make the prior distribution of these symbols a design choice. The recent IR-Net of Qin et al. argues that imposing a Bernoulli distribution with equal priors (equal bit ratios) over the binary weights leads to maximum entropy and thus minimizes information loss. However, prior work cannot precisely control the binary weight distribution during training, and therefore cannot guarantee maximum entropy. Here, we show that quantizing using optimal transport can guarantee any bit ratio, including equal ratios. We investigate experimentally that equal bit ratios are indeed preferable and show that our method leads to optimization benefits. We show that our quantization method is effective when compared to state-of-the-art binarization methods, even when using binary weight pruning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge