Entropy-Constrained Training of Deep Neural Networks
Paper and Code
Dec 19, 2018
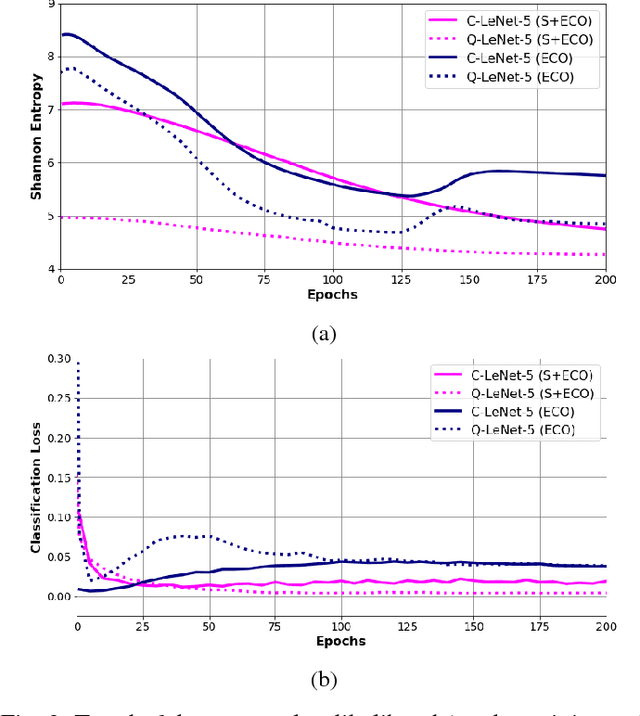
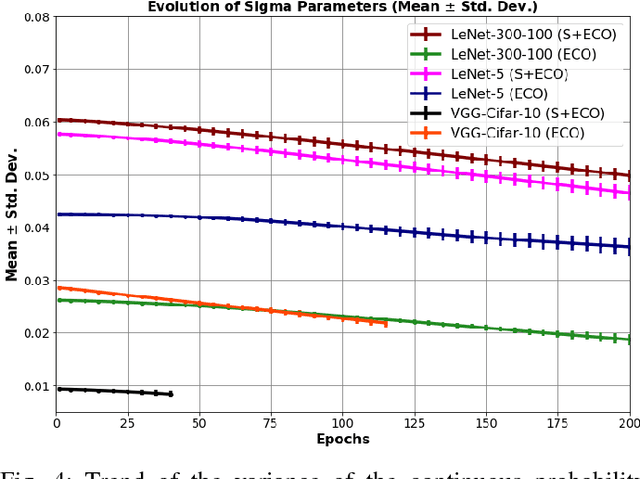
We propose a general framework for neural network compression that is motivated by the Minimum Description Length (MDL) principle. For that we first derive an expression for the entropy of a neural network, which measures its complexity explicitly in terms of its bit-size. Then, we formalize the problem of neural network compression as an entropy-constrained optimization objective. This objective generalizes many of the compression techniques proposed in the literature, in that pruning or reducing the cardinality of the weight elements of the network can be seen special cases of entropy-minimization techniques. Furthermore, we derive a continuous relaxation of the objective, which allows us to minimize it using gradient based optimization techniques. Finally, we show that we can reach state-of-the-art compression results on different network architectures and data sets, e.g. achieving x71 compression gains on a VGG-like architecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge