Ensemble Methods for Multi-label Classification
Paper and Code
Jul 06, 2013
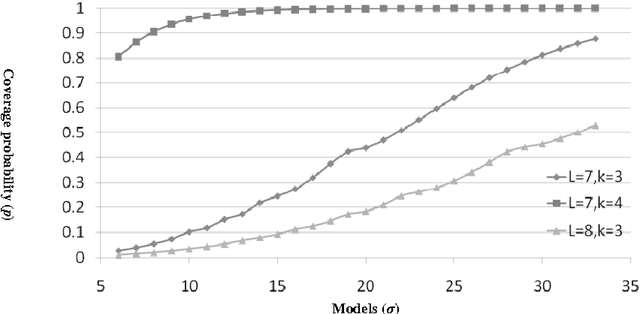
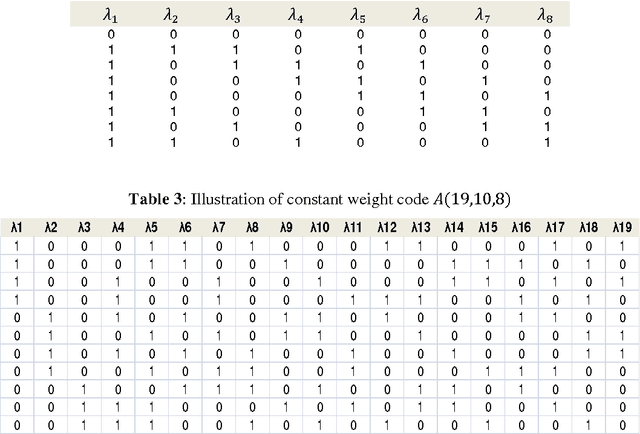

Ensemble methods have been shown to be an effective tool for solving multi-label classification tasks. In the RAndom k-labELsets (RAKEL) algorithm, each member of the ensemble is associated with a small randomly-selected subset of k labels. Then, a single label classifier is trained according to each combination of elements in the subset. In this paper we adopt a similar approach, however, instead of randomly choosing subsets, we select the minimum required subsets of k labels that cover all labels and meet additional constraints such as coverage of inter-label correlations. Construction of the cover is achieved by formulating the subset selection as a minimum set covering problem (SCP) and solving it by using approximation algorithms. Every cover needs only to be prepared once by offline algorithms. Once prepared, a cover may be applied to the classification of any given multi-label dataset whose properties conform with those of the cover. The contribution of this paper is two-fold. First, we introduce SCP as a general framework for constructing label covers while allowing the user to incorporate cover construction constraints. We demonstrate the effectiveness of this framework by proposing two construction constraints whose enforcement produces covers that improve the prediction performance of random selection. Second, we provide theoretical bounds that quantify the probabilities of random selection to produce covers that meet the proposed construction criteria. The experimental results indicate that the proposed methods improve multi-label classification accuracy and stability compared with the RAKEL algorithm and to other state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge