Enhanced 3DTV Regularization and Its Applications on Hyper-spectral Image Denoising and Compressed Sensing
Paper and Code
Sep 18, 2018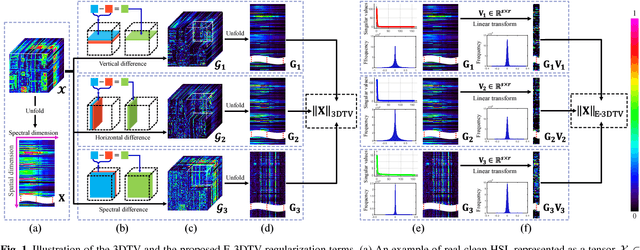
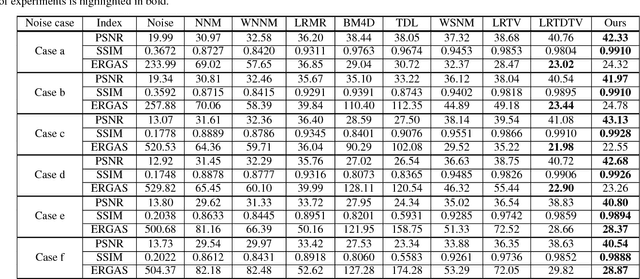
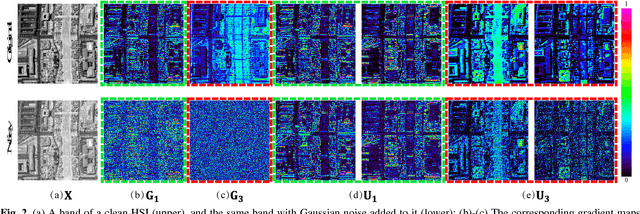
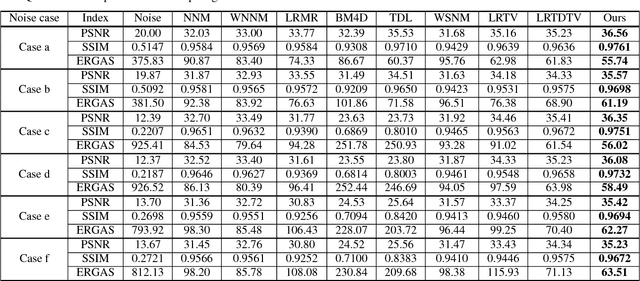
The 3-D total variation (3DTV) is a powerful regularization term, which encodes the local smoothness prior structure underlying a hyper-spectral image (HSI), for general HSI processing tasks. This term is calculated by assuming identical and independent sparsity structures on all bands of gradient maps calculated along spatial and spectral HSI modes. This, however, is always largely deviated from the real cases, where the gradient maps are generally with different while correlated sparsity structures across all their bands. Such deviation tends to hamper the performance of the related method by adopting such prior term. To this is- sue, this paper proposes an enhanced 3DTV (E-3DTV) regularization term beyond conventional 3DTV. Instead of imposing sparsity on gradient maps themselves, the new term calculated sparsity on the subspace bases on the gradient maps along their bands, which naturally encode the correlation and difference across these bands, and more faithfully reflect the insightful configurations of an HSI. The E-3DTV term can easily replace the previous 3DTV term and be em- bedded into an HSI processing model to ameliorate its performance. The superiority of the proposed methods is substantiated by extensive experiments on two typical related tasks: HSI denoising and compressed sensing, as compared with state-of-the-arts designed for both tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge