Engineering flexible machine learning systems by traversing functionally invariant paths in weight space
Paper and Code
May 09, 2022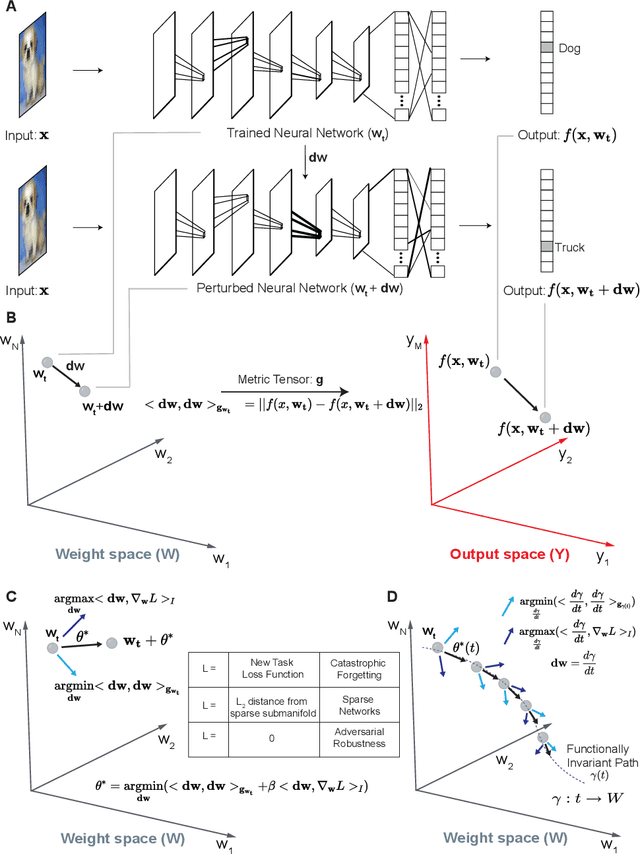
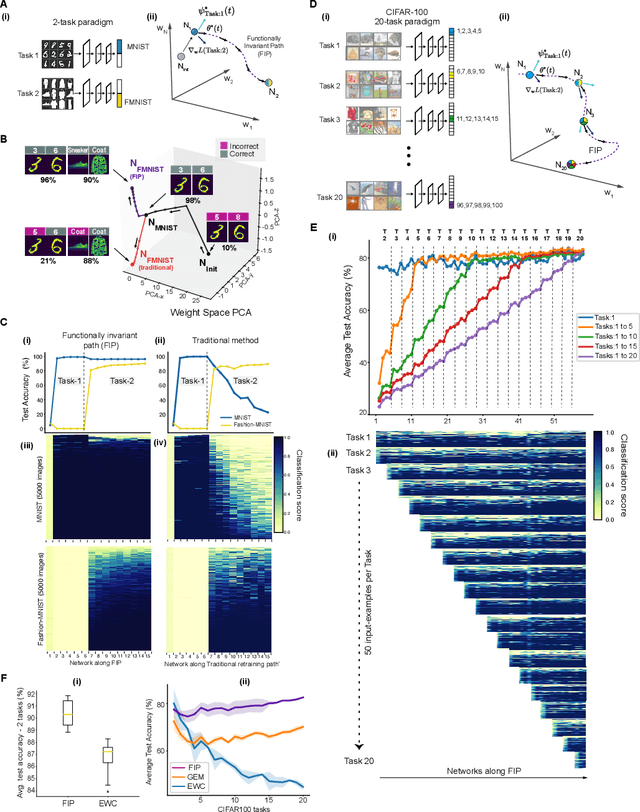
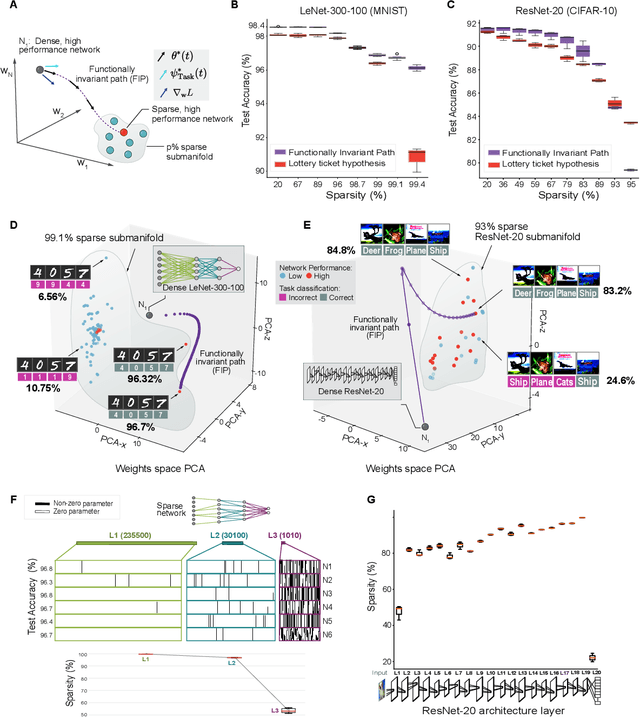

Deep neural networks achieve human-like performance on a variety of perceptual and decision making tasks. However, deep networks perform poorly when confronted with changing tasks or goals, and broadly fail to match the flexibility and robustness of human intelligence. Here, we develop a mathematical and algorithmic framework that enables continual training of deep neural networks on a broad range of objectives by defining path connected sets of neural networks that achieve equivalent functional performance on a given machine learning task while modulating network weights to achieve high-performance on a secondary objective. We view the weight space of a neural network as a curved Riemannian manifold and move a neural network along a functionally invariant path in weight space while searching for networks that satisfy a secondary objective. We introduce a path-sampling algorithm that trains networks with millions of weight parameters to learn a series of image classification tasks without performance loss. The algorithm generalizes to accommodate a range of secondary objectives including weight-pruning and weight diversification and exhibits state of the art performance on network compression and adversarial robustness benchmarks. Broadly, we demonstrate how the intrinsic geometry of machine learning problems can be harnessed to construct flexible and robust neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge