Energy-Inspired Models: Learning with Sampler-Induced Distributions
Paper and Code
Oct 31, 2019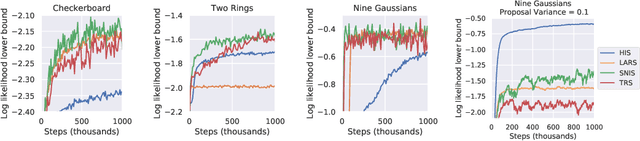
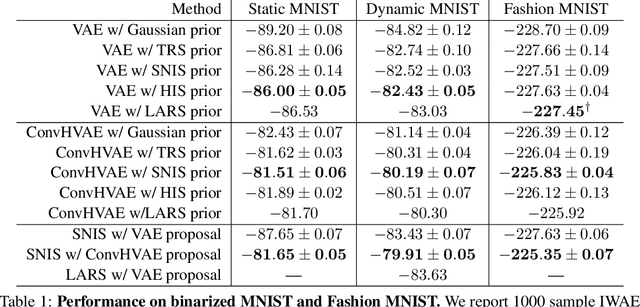
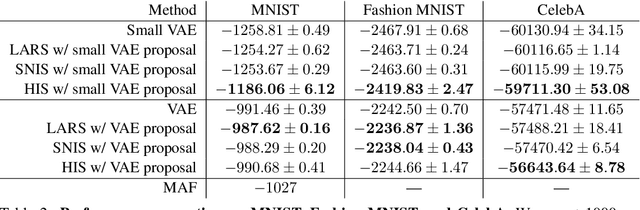
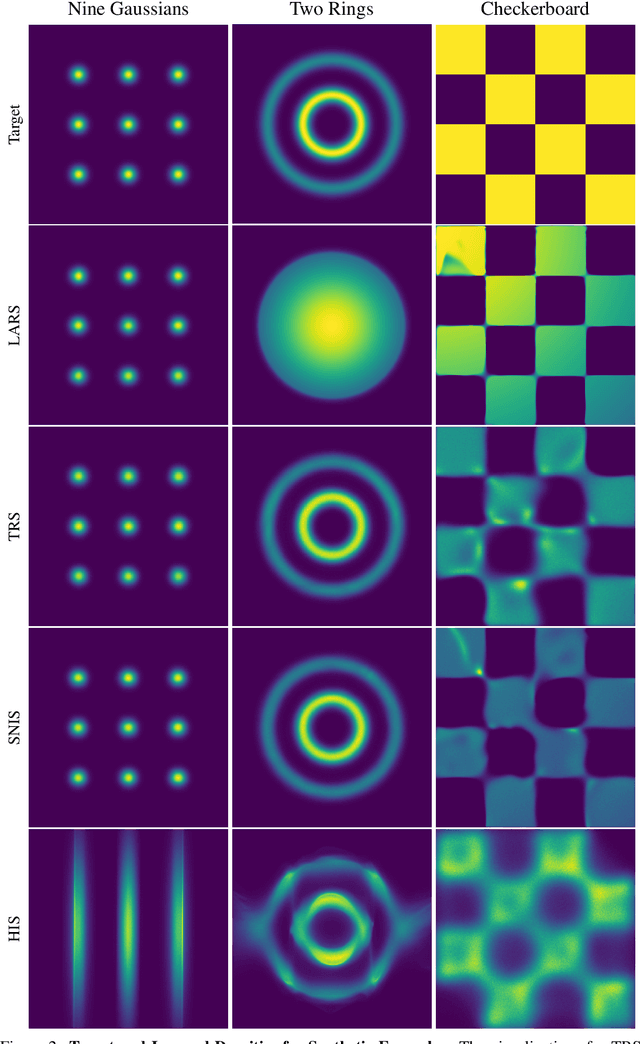
Energy-based models (EBMs) are powerful probabilistic models, but suffer from intractable sampling and density evaluation due to the partition function. As a result, inference in EBMs relies on approximate sampling algorithms, leading to a mismatch between the model and inference. Motivated by this, we consider the sampler-induced distribution as the model of interest and maximize the likelihood of this model. This yields a class of energy-inspired models (EIMs) that incorporate learned energy functions while still providing exact samples and tractable log-likelihood lower bounds. We describe and evaluate three instantiations of such models based on truncated rejection sampling, self-normalized importance sampling, and Hamiltonian importance sampling. These models outperform or perform comparably to the recently proposed Learned Accept/Reject Sampling algorithm and provide new insights on ranking Noise Contrastive Estimation and Contrastive Predictive Coding. Moreover, EIMs allow us to generalize a recent connection between multi-sample variational lower bounds and auxiliary variable variational inference. We show how recent variational bounds can be unified with EIMs as the variational family.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge