Encoding Defensive Driving as a Dynamic Nash Game

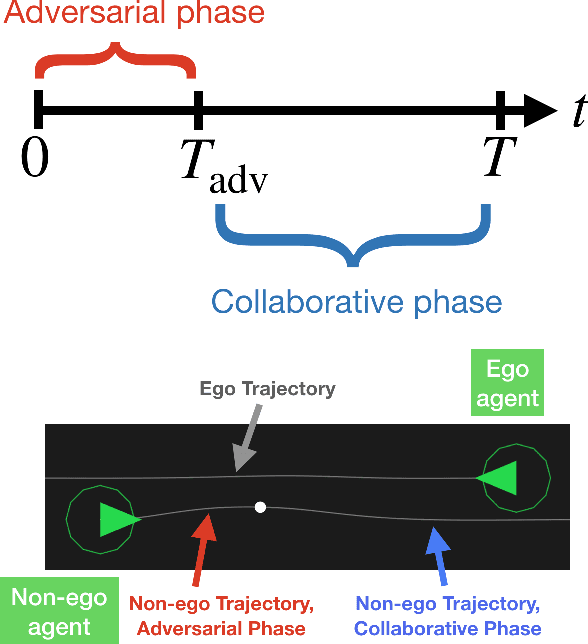
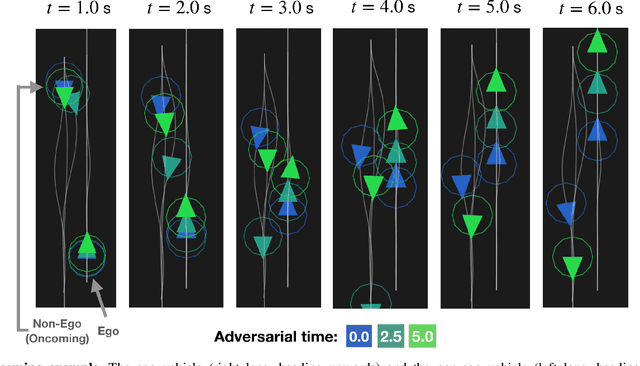
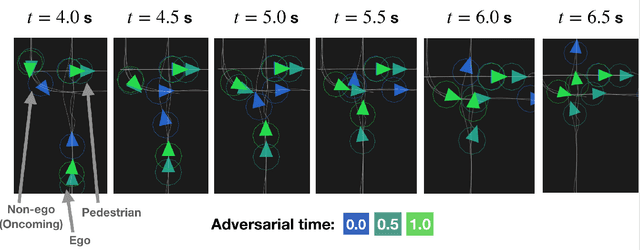
Robots deployed in real-world environments should operate safely in a robust manner. In scenarios where an "ego" agent navigates in an environment with multiple other "non-ego" agents, two modes of safety are commonly proposed: adversarial robustness and probabilistic constraint satisfaction. However, while the former is generally computationally-intractable and leads to overconservative solutions, the latter typically relies on strong distributional assumptions and ignores strategic coupling between agents. To avoid these drawbacks, we present a novel formulation of robustness within the framework of general sum dynamic game theory, modeled on defensive driving. More precisely, we inject the ego's cost function with an adversarial phase, a time interval during which other agents are assumed to be temporarily distracted, to robustify the ego agent's trajectory against other agents' potentially dangerous behavior during this time. We demonstrate the effectiveness of our new formulation in encoding safety via multiple traffic scenarios.