Empirical Frequentist Coverage of Deep Learning Uncertainty Quantification Procedures
Paper and Code
Oct 06, 2020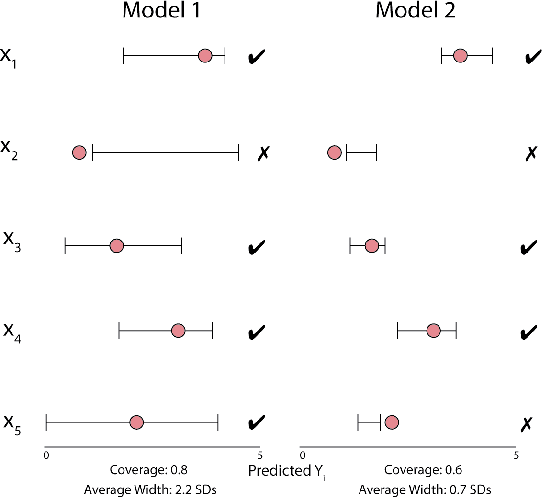
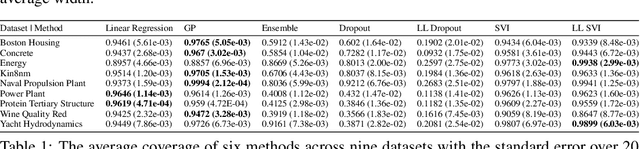

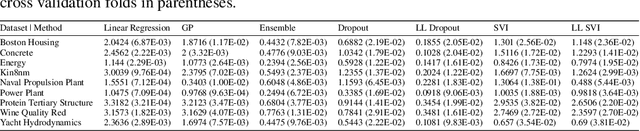
Uncertainty quantification for complex deep learning models is increasingly important as these techniques see growing use in high-stakes, real-world settings. Currently, the quality of a model's uncertainty is evaluated using point-prediction metrics such as negative log-likelihood or the Brier score on heldout data. In this study, we provide the first large scale evaluation of the empirical frequentist coverage properties of well known uncertainty quantification techniques on a suite of regression and classification tasks. We find that, in general, some methods do achieve desirable coverage properties on in distribution samples, but that coverage is not maintained on out-of-distribution data. Our results demonstrate the failings of current uncertainty quantification techniques as dataset shift increases and establish coverage as an important metric in developing models for real-world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge