Empirical Evaluation of Biased Methods for Alpha Divergence Minimization
Paper and Code
May 13, 2021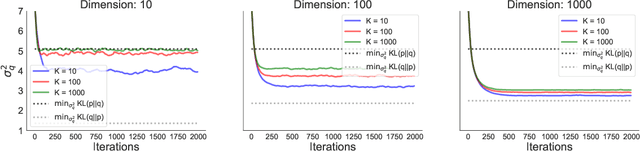
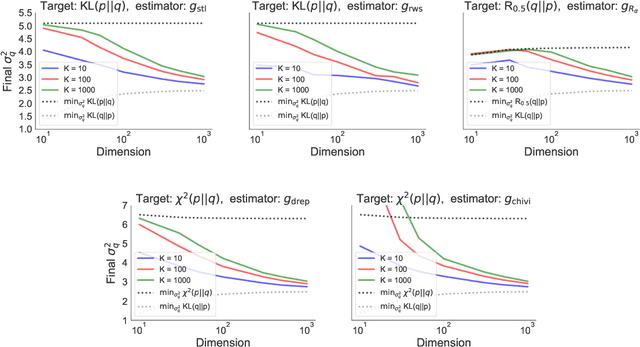
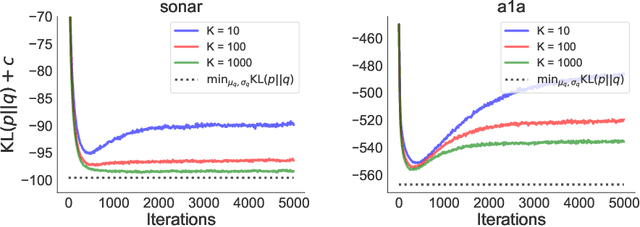
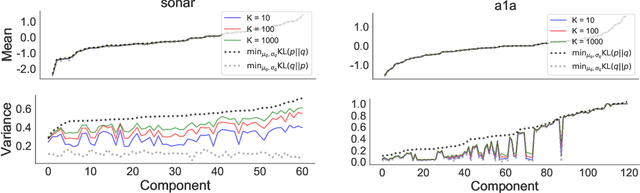
In this paper we empirically evaluate biased methods for alpha-divergence minimization. In particular, we focus on how the bias affects the final solutions found, and how this depends on the dimensionality of the problem. We find that (i) solutions returned by these methods appear to be strongly biased towards minimizers of the traditional "exclusive" KL-divergence, KL(q||p), and (ii) in high dimensions, an impractically large amount of computation is needed to mitigate this bias and obtain solutions that actually minimize the alpha-divergence of interest.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge