Eliminating Sharp Minima from SGD with Truncated Heavy-tailed Noise
Paper and Code
Feb 08, 2021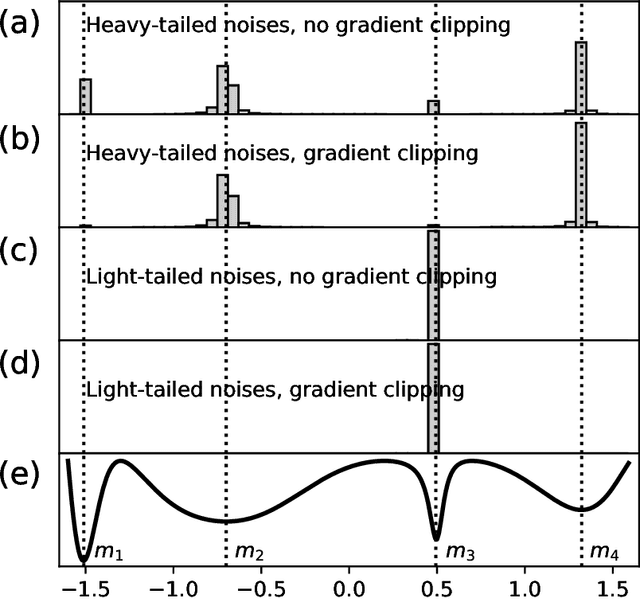
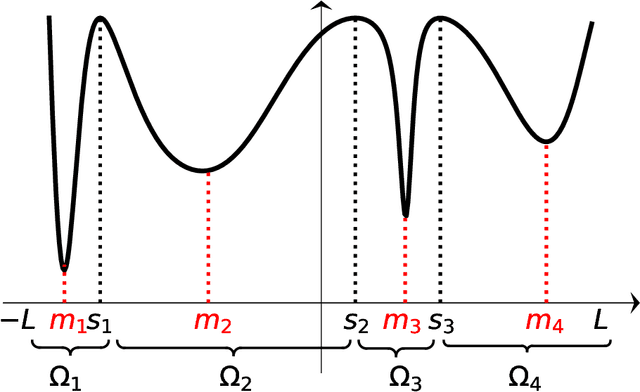
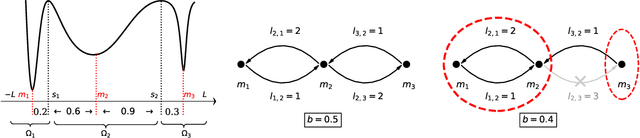
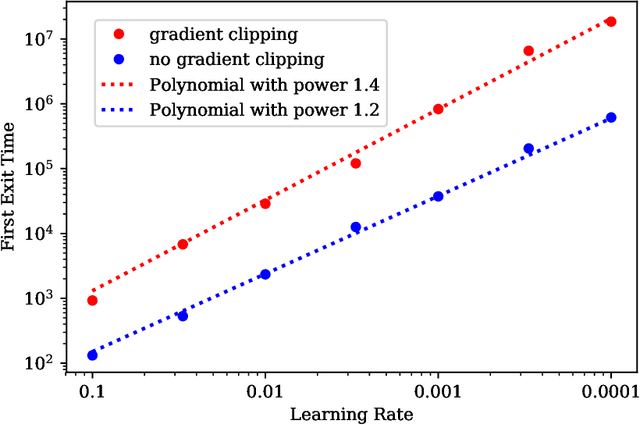
The empirical success of deep learning is often attributed to SGD's mysterious ability to avoid sharp local minima in the loss landscape, which is well known to lead to poor generalization. Recently, empirical evidence of heavy-tailed gradient noise was reported in many deep learning tasks; under the presence of such heavy-tailed noise, it can be shown that SGD can escape sharp local minima, providing a partial solution to the mystery. In this work, we analyze a popular variant of SGD where gradients are truncated above a fixed threshold. We show that it achieves a stronger notion of avoiding sharp minima; it can effectively eliminate sharp local minima entirely from its training trajectory. We characterize the dynamics of truncated SGD driven by heavy-tailed noises. First, we show that the truncation threshold and width of the attraction field dictate the order of the first exit time from the associated local minimum. Moreover, when the objective function satisfies appropriate structural conditions, we prove that as the learning rate decreases the dynamics of the heavy-tailed SGD closely resemble that of a special continuous-time Markov chain which never visits any sharp minima. We verify our theoretical results with numerical experiments and discuss the implications on the generalizability of SGD in deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge