Electronic excited states in deep variational Monte Carlo
Paper and Code
Mar 17, 2022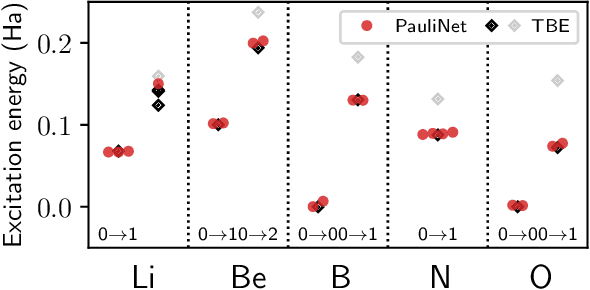
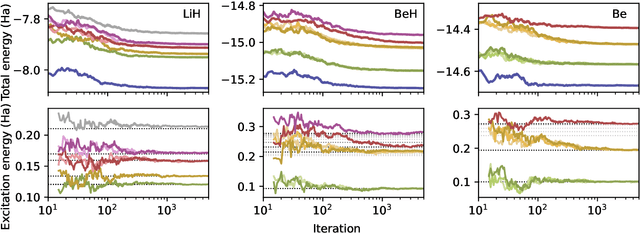
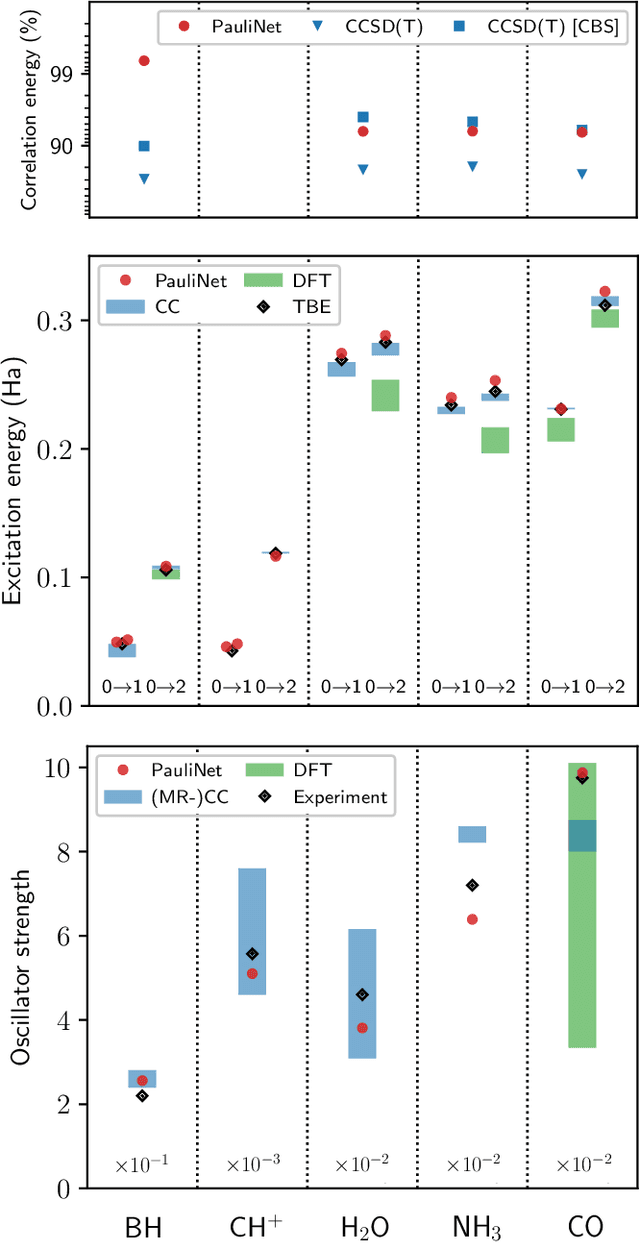
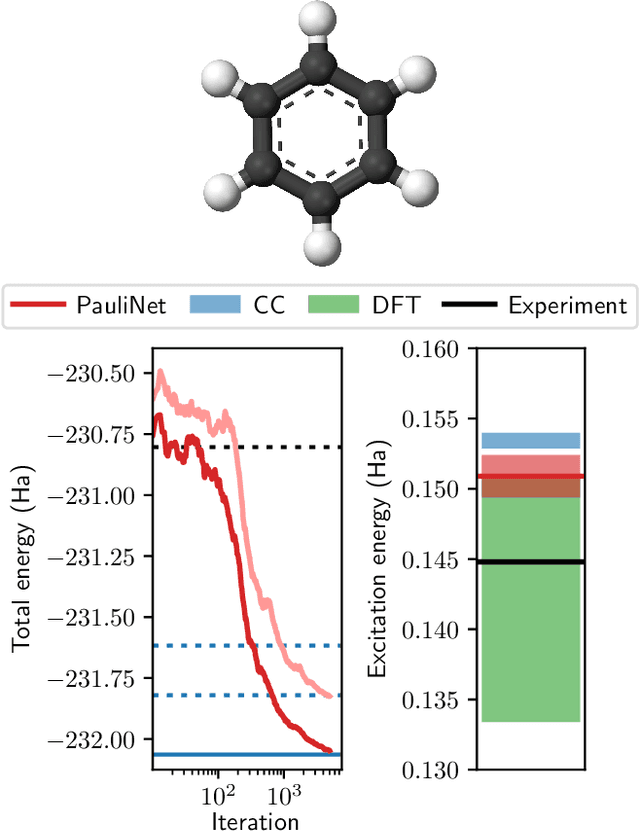
Obtaining accurate ground and low-lying excited states of electronic systems is crucial in a multitude of important applications. One ab initio method for solving the electronic Schr\"odinger equation that scales favorably for large systems and whose accuracy is limited only by the choice of wavefunction ansatz employed is variational quantum Monte Carlo (QMC). The recently introduced deep QMC approach, using a new class of ansatzes represented by deep neural networks, has been shown to generate nearly exact ground-state solutions for molecules containing up to a few dozen electrons, with the potential to scale to much larger systems where other highly accurate methods are not feasible. In this paper, we advance one such ansatz (PauliNet) to compute electronic excited states through a simple variational procedure. We demonstrate our method on a variety of small atoms and molecules where we consistently achieve high accuracy for low-lying states. To highlight the method's potential for larger systems, we show that for the benzene molecule, PauliNet is on par with significantly more expensive high-level electronic structure methods in terms of the excitation energy and outperforms them in terms of absolute energies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge