Efficient Touch Based Localization through Submodularity
Paper and Code
Apr 23, 2013
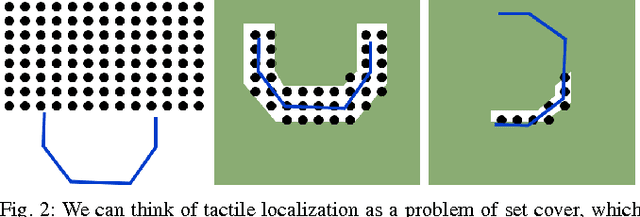
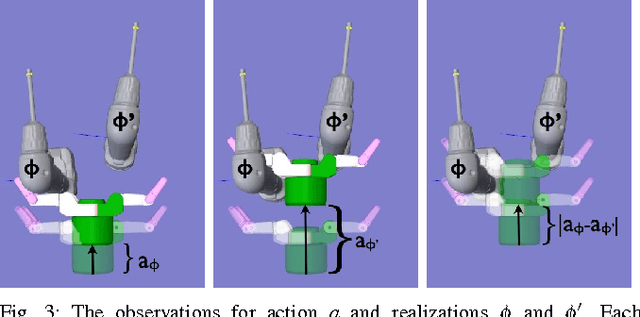
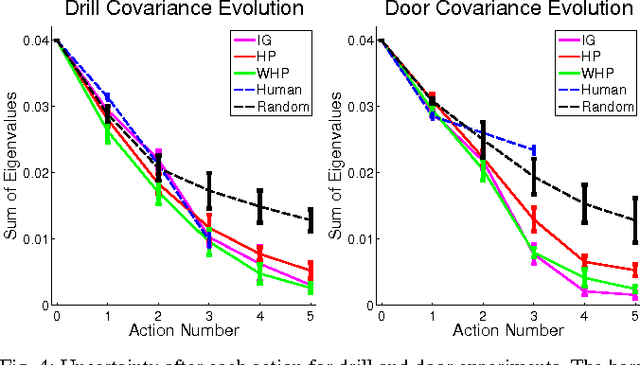
Many robotic systems deal with uncertainty by performing a sequence of information gathering actions. In this work, we focus on the problem of efficiently constructing such a sequence by drawing an explicit connection to submodularity. Ideally, we would like a method that finds the optimal sequence, taking the minimum amount of time while providing sufficient information. Finding this sequence, however, is generally intractable. As a result, many well-established methods select actions greedily. Surprisingly, this often performs well. Our work first explains this high performance -- we note a commonly used metric, reduction of Shannon entropy, is submodular under certain assumptions, rendering the greedy solution comparable to the optimal plan in the offline setting. However, reacting online to observations can increase performance. Recently developed notions of adaptive submodularity provide guarantees for a greedy algorithm in this online setting. In this work, we develop new methods based on adaptive submodularity for selecting a sequence of information gathering actions online. In addition to providing guarantees, we can capitalize on submodularity to attain additional computational speedups. We demonstrate the effectiveness of these methods in simulation and on a robot.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge