Efficient Subgraph Isomorphism using Graph Topology

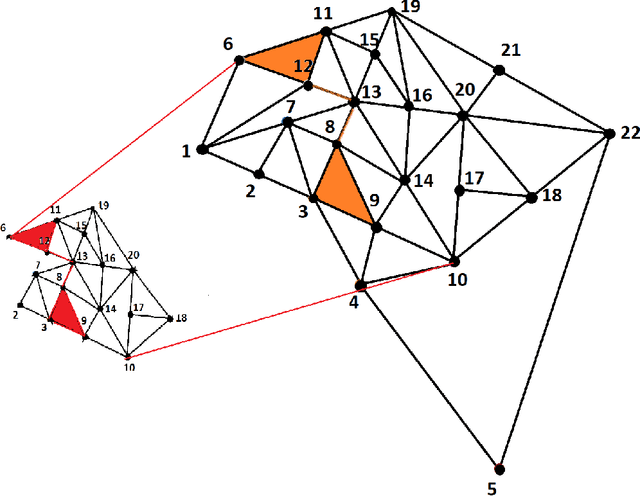
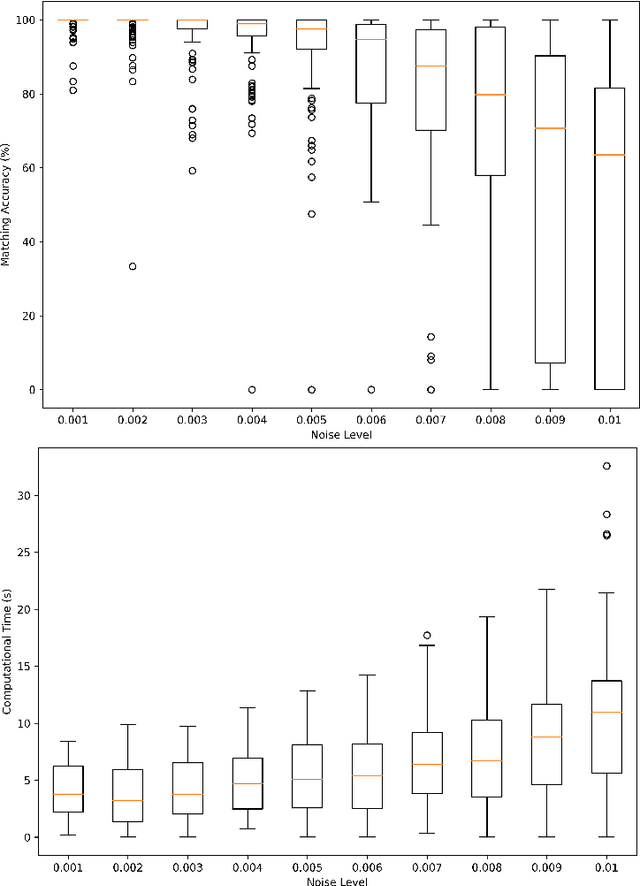
Subgraph isomorphism or subgraph matching is generally considered as an NP-complete problem, made more complex in practical applications where the edge weights take real values and are subject to measurement noise and possible anomalies. To the best of our knowledge, almost all subgraph matching methods utilize node labels to perform node-node matching. In the absence of such labels (in applications such as image matching and map matching among others), these subgraph matching methods do not work. We propose a method for identifying the node correspondence between a subgraph and a full graph in the inexact case without node labels in two steps - (a) extract the minimal unique topology preserving subset from the subgraph and find its feasible matching in the full graph, and (b) implement a consensus-based algorithm to expand the matched node set by pairing unique paths based on boundary commutativity. Going beyond the existing subgraph matching approaches, the proposed method is shown to have realistically sub-linear computational efficiency, robustness to random measurement noise, and good statistical properties. Our method is also readily applicable to the exact matching case without loss of generality. To demonstrate the effectiveness of the proposed method, a simulation and a case study is performed on the Erdos-Renyi random graphs and the image-based affine covariant features dataset respectively.